Question

【题目】如右图所示，一玻璃砖的截面为直角三角形ABC，其中，AB=9cm；现有两细束平行且相同的单色光a、b，分别从AC边上的D点、E点以角入射，且均能从AB边上的F点射出，已知AD=AF=3cm，求：

（i）玻璃砖的折射率；

（ii）D、E两点之间的距离。

Answer 1

【答案】（i），（ii）12cm.

【解析】试题分析：（i）由题意画出光路图，由数学知识求出入射光a经AC边的折射角，再由折射定律求玻璃砖的折射率．（ii）根据求出全反射临界角C，可知光线在BC边上发生了全反射，由几何知识求出D、E两点之间的距离．

（i）作出的光路图如图所示

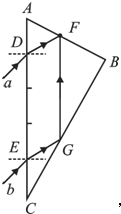
由于AD=AF， ，则入射光a经AC边的折射角为：

玻璃砖的折射率为：

（ii）设光在玻璃砖中发生全反射的临界角为C

则有：

解得：

由图可知，b光经AC边折射后，在BC边上的入射角为，大于临界角C

所以此光线在G点发生了全反射

由几何知识可知，四边形DEGF是平行四边形，由于，AF=3cm

则有：

且，又 FG=DE

联立解得：DE=12cm