题目内容
【题目】如图所示,一轻质弹簧上端悬挂于天花板,下端系一质量为m1=2.0kg的物体A , 平衡时物体A距天花板h1=0.60m . 在距物体A正上方高为h=0.45m处有一个质量为m2=1.0kg的物体B , 由静止释放B , 下落过程某时刻与弹簧下端的物体A碰撞(碰撞时间极短)并立即以相同的速度运动.已知两物体不粘连,且可视为质点.g=L0m/s2 . 求: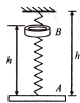
(1)碰撞结束瞬间两物体的速度大小;
(2)碰撞结束后两物体一起向下运动,历时0.25s第一次到达最低点.求在该过程中,两物体间的平均作用力.
【答案】
(1)
B物体自由下落至与A碰撞前其速度为v0,根据自由落体运动规律,有: ![]()
AB碰撞结束之后瞬时二者速度共同速度为vt,以向下为正方向,根据动量守恒定律,有:
m2v0=(m1+m2)vt
解得:
vt=1.0m/s
(2)
选择竖直向下为正方向,从二者一起运动到速度变为零的过程中,选择B作为研究对象,根据动量定理,有:
(m2g﹣N)t=0﹣m2vt
解得N=14N,方向竖直向上
【解析】(I)物体B碰撞前做自由落体运动,根据速度位移公式求解末速度;碰撞过程系统动量守恒,根据动量守恒定律列式求解共同速度;
(II)对物体B的下降过程根据动量定理列式求解平均弹力.
【考点精析】掌握动量定理和动量守恒定律是解答本题的根本,需要知道动量定理的研究对象可以是单个物体,也可以是物体系统.对物体系统,只需分析系统受的外力,不必考虑系统内力.系统内力的作用不改变整个系统的总动量;动量定理不仅适用于恒定的力,也适用于随时间变化的力.对于变力,动量定理中的力F应当理解为变力在作用时间内的平均值;动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.