题目内容
19.图1所示为足够大空间内存在水平方向的匀强磁场,在磁场中A、B两物块叠在一起置于光滑水平面上,物块A带正电,物块B不带电且表面绝缘,A、B接触面粗糙.自t=0时刻起用水平恒力F作用在物块B上,由静止开始做匀加速直线运动.图2图象的横轴表示时间,则纵轴y可以表示( )
| A. | A所受洛伦兹力大小 | B. | A物块加速度大小 | ||
| C. | A对B压力大小 | D. | A对B的摩擦力大小 |
分析 对整体分析,运用牛顿第二定律得出加速度,判断出整体的运动规律,然后求出洛伦兹力与时间的变化关系;运用隔离法求出A对B的摩擦力的大小、A对B的压力大小.
解答 解:A、物体由静止做匀加速运动,速度v=at;故洛伦兹力:F=qvB=qBat,洛伦兹力大小随时间t变化的应过原点,故A错误.
B、物块A对物块B的摩擦力大小f=mAa,所以f随时间t的变化保持不变,故B错误.
C、A对B的压力:N=mAg+qvB=mAg+qBat,故C正确.
D、由牛顿第二定律可知,物块A对物块B的摩擦力大小f=mAa,保持不变.故D错误.
故选:C.
点评 该题考查带电物体在复合场中的运动,解决本题的关键能够正确地进行受力分析,运用牛顿第二定律进行求解,以及注意整体法和隔离法的运用.

练习册系列答案
相关题目
9. 在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图甲所示.振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成了如图乙所示的波形图,则该波的周期T、波速υ分别是( )(填入选项前的字母,有填错的不得分)
在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图甲所示.振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成了如图乙所示的波形图,则该波的周期T、波速υ分别是( )(填入选项前的字母,有填错的不得分)
 在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图甲所示.振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成了如图乙所示的波形图,则该波的周期T、波速υ分别是( )(填入选项前的字母,有填错的不得分)
在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图甲所示.振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成了如图乙所示的波形图,则该波的周期T、波速υ分别是( )(填入选项前的字母,有填错的不得分)| A. | T=$\frac{t}{2}$,υ=$\frac{16a}{t}$ | B. | T=$\frac{2}{3}$t,υ=$\frac{12a}{t}$ | C. | T=t,υ=$\frac{8a}{t}$ | D. | T=$\frac{3}{4}$t,υ=$\frac{6a}{t}$ |
10. 一列简谐横波沿x轴正向传播,O、A、B、C、D为传播方向上的五个质点,相邻质点之间相隔1.0m,如图所示.t=0时刻波源O点开始向y轴正方向运动.经过0.10s它第一次达到正向最大位移,而此时刻B质点开始从平衡位置开始向y轴正方向运动.由此可以确定( )
一列简谐横波沿x轴正向传播,O、A、B、C、D为传播方向上的五个质点,相邻质点之间相隔1.0m,如图所示.t=0时刻波源O点开始向y轴正方向运动.经过0.10s它第一次达到正向最大位移,而此时刻B质点开始从平衡位置开始向y轴正方向运动.由此可以确定( )
 一列简谐横波沿x轴正向传播,O、A、B、C、D为传播方向上的五个质点,相邻质点之间相隔1.0m,如图所示.t=0时刻波源O点开始向y轴正方向运动.经过0.10s它第一次达到正向最大位移,而此时刻B质点开始从平衡位置开始向y轴正方向运动.由此可以确定( )
一列简谐横波沿x轴正向传播,O、A、B、C、D为传播方向上的五个质点,相邻质点之间相隔1.0m,如图所示.t=0时刻波源O点开始向y轴正方向运动.经过0.10s它第一次达到正向最大位移,而此时刻B质点开始从平衡位置开始向y轴正方向运动.由此可以确定( )| A. | 这列波的波长为8.0m | |
| B. | 周期为1.0s | |
| C. | 这列波的波速为20m/s,频率是2.5Hz | |
| D. | 在0.30s末D质点刚开始振动 | |
| E. | 在0.30s末D质点第一次达到正向最大位移 |
7.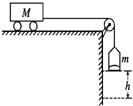 如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )
如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )
 如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )
如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )| A. | 绳拉车的力始终为mg | |
| B. | 当M远远大于m时,才可以认为绳拉车的力为mg | |
| C. | 小车获得的动能为$\frac{Mmgh}{M+m}$ | |
| D. | 小车获得的动能为mgh |
14. 一个倾角为θ(0°<θ<90°)的光滑斜面固定在竖直的光滑墙壁上,一铁球在一水平推力F作用下静止于墙壁与斜面之间,与斜面的接触点为A,如图所示.已知球的半径为R,推力F的作用线过球心,则下列判断正确的是( )
一个倾角为θ(0°<θ<90°)的光滑斜面固定在竖直的光滑墙壁上,一铁球在一水平推力F作用下静止于墙壁与斜面之间,与斜面的接触点为A,如图所示.已知球的半径为R,推力F的作用线过球心,则下列判断正确的是( )
 一个倾角为θ(0°<θ<90°)的光滑斜面固定在竖直的光滑墙壁上,一铁球在一水平推力F作用下静止于墙壁与斜面之间,与斜面的接触点为A,如图所示.已知球的半径为R,推力F的作用线过球心,则下列判断正确的是( )
一个倾角为θ(0°<θ<90°)的光滑斜面固定在竖直的光滑墙壁上,一铁球在一水平推力F作用下静止于墙壁与斜面之间,与斜面的接触点为A,如图所示.已知球的半径为R,推力F的作用线过球心,则下列判断正确的是( )| A. | 推力F增大,斜面对球的支持力一定增大 | |
| B. | 斜面对球的支持力一定大于球的重力 | |
| C. | 推力F的最小值等于Gcotθ | |
| D. | 推力F增大,地面对斜面的支持力不变 |
 如图所示,M、N为两块水平放置的平行金属板,长为L,相距为2d,当S断开时(两板未充电),一带电量为+q,质量为m的油滴,以一水平初速度从两板间中点p飞入,恰好落到下板的中点Q处.求:
如图所示,M、N为两块水平放置的平行金属板,长为L,相距为2d,当S断开时(两板未充电),一带电量为+q,质量为m的油滴,以一水平初速度从两板间中点p飞入,恰好落到下板的中点Q处.求: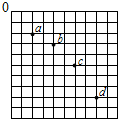 在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的一部分轨迹,已知图中小方格的边长L=10cm,则小球平抛的初速度大小为v0=2m/s(取g=10m/s2),小球的抛出点坐标为(0.1m,0.1875m).
在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的一部分轨迹,已知图中小方格的边长L=10cm,则小球平抛的初速度大小为v0=2m/s(取g=10m/s2),小球的抛出点坐标为(0.1m,0.1875m). 如图所示,在半径为R的洗衣机圆桶内,有质量为m的一件衣服贴着内壁跟随桶以角速度ω做匀速圆周运动,求:
如图所示,在半径为R的洗衣机圆桶内,有质量为m的一件衣服贴着内壁跟随桶以角速度ω做匀速圆周运动,求: 如图所示,一个匝数n=30的矩形线框可能垂直于磁场的轴OO′匀速转动,线圈面积为0.02m2,磁感应强度的大小B=2T,角速度ω=100rad/s.若从线圈经过中性面开始计时,试求:
如图所示,一个匝数n=30的矩形线框可能垂直于磁场的轴OO′匀速转动,线圈面积为0.02m2,磁感应强度的大小B=2T,角速度ω=100rad/s.若从线圈经过中性面开始计时,试求: