Question

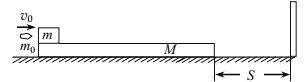
【题目】如图所示，光滑的水平面上静止一个足够长的木板，质量为M=4kg木板的左端放一个质量为m=0.9kg的小木块（可看成质点）木块与木板间的动摩擦因数为μ=0.2.距木板右端S=0.81m处固定一个竖直弹性挡板，木板与挡板碰撞时没有能量损失。一颗质量为m0=100g的子弹以速度v0=50m/s水平击中木块且留在其中。求∶

(1)子弹击中木块瞬间，木块的速度；

(2)木板与挡板碰撞时木块的速度大小；

(3)最终木板的速度大小和方向；

(3)木块相对木板滑行的最大位移（结果保留1位有效数字）。

Answer 1

【答案】(1)5m/s；(2)1.4m/s；(3)-0.44m/s，方向向左；(4)6m

【解析】

(1)设子弹击中木块后与木块的共同速度为v1取向右为正方向，由动量守恒定律知

代入数据得

v1=5m/s

(2)子弹击中木块以后与木块一起向右减速，同时木板向右加速运动，设经过时间t后恰达到共同速度v，由动量守值定律

（m0+m）v1=(m0+m+M）v

代入数据得

v=1m/s

对木板，由牛顿第二定律

由运动学公式得

则木板在t时间内向右运动的位移

由于x>S，可知木板在与木块达到共同速度之前就已经和弹性板相撞

设木板与弹性挡板相撞前速度为v3，木块的速度为v2

对木板，运动学公式

得

v3=0.9m/s

由动量守值定律

（m0+m）v1=(m0+m）v2+Mv3

代入上式得

v2=1.4m/s

(3)碰后木板的动量向左，大小为

p=Mv3=3.6kgm/s

木块的动量向右，大小为

p′=(m0+m）v2=1.4kgm/s

因此，木块与板相对滑动后，最终一起向左以共同速度v′做匀速直线运动。

由动量守恒定律知

（m0+m）v2-Mv3=(m0+m+M）v′

代入数据得

v′=-0.44m/s

方向向左

(4)设木块相对木板滑行的最大位移为L，由木块与木板相对滑动全过程中能量守恒知∶

得

L=6m