Question

【题目】如图所示，固定的锥形漏斗内壁是光滑的，内壁上有两个质量相等的小球A和B，在各自不同的水平面做匀速圆周运动，以下说法正确的是（ ）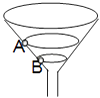

A.VA＞VB
B.ωA＞ωB
C.aA＞aB
D.压力NA＞NB

Answer 1

【答案】A
【解析】解：研究任意一个小球：受力如图．将FN沿水平和竖直方向分解得：
FNcosθ=ma…①
FNsinθ=mg…②．
由②可知支持力相等，则A、B对内壁的压力大小相等：NA=NB ．
根据牛顿第二定律，合外力提供向心力，合外力相等，则向心力相等．由①②可得：
mgcotθ=ma=m =mω2r．可知半径大的线速度大，角速度小．
则A的线速度大于B的线速度，VA＞VB ， A的角速度小于B的角速度，ωA＜ωB ．
向心加速度 a=gcotθ，则知两球的向心加速度相等，aA=aB ． 故A正确，B、C、D错误．
故选：A．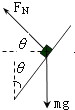

【考点精析】认真审题，首先需要了解向心力(向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力)．