Question

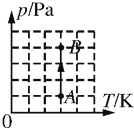
【题目】如图甲所示，截面积为0.2m2的100匝圆形线圈A处在变化的磁场中．磁场方向垂直纸面，其磁感应强度B随时间t的变化规律如图乙所示，设向外为B的正方向．R1=4Ω，R2=6Ω，C=30 μF，线圈的内阻不计，求电容器上极板所带电荷量并说明正负．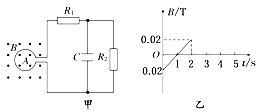

Answer 1

【答案】解：根据图像，结合题意可知，在0到1秒内，磁场方向向里，且大小减小，由楞次定律，则有线圈产生顺时针的电流，从而给电容器充电，电容器上极板带正电；
在1秒到2秒内，磁场方向向外，大小在增大，由楞次定律，则有线圈产生顺时针的电流，仍给电容器充电，则电容器上极板带正电；由法拉第电磁感应定律，得：
E= = V=0.4V；
由电路图可得：UR2= R2= ×6V=0.24V；
因电容器与电阻R2并联，则电压相等，根据电容与电量关系式，则有：
Q=CUC=30×10﹣6×0.24C=7.2×10﹣6 C；
答：电容器上极板所带电荷量7.2×10﹣6 C，且电容器上极板带正电
【解析】根据E=n 求出感应电动势的大小，再根据闭合电路欧姆定律求出电流的大小，从而求出电容器充电时的电压，再根据Q=CU求出电容器所带的电量．
【考点精析】根据题目的已知条件，利用楞次定律的相关知识可以得到问题的答案，需要掌握楞次定律适用于一般情况的感应电流方向的判定，而右手定则只适用于导线切割磁感线运动的情况，此种情况用右手定则判定比用楞次定律判定简便．