题目内容
13.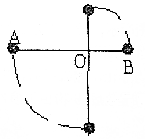 如图所示,一轻细杆两端分别固定着两只质址均为m的小球,O点为光滑水平轴,已知AO=2L,BO=L,轻杆水平时无初速释放小球至轻杆竖直位置过程中,不计空气阻力.
如图所示,一轻细杆两端分别固定着两只质址均为m的小球,O点为光滑水平轴,已知AO=2L,BO=L,轻杆水平时无初速释放小球至轻杆竖直位置过程中,不计空气阻力.求:(1)A球的重力势能减小多少?B球的重力势能增加多少?系统的重力势能减小多少?
(2)转到竖直位置时A、B两球的速度为多少?
(3)A球对细杆的拉力多大?
分析 (1)明确两球高度的变化,根据重力势能的定义可分析重力势能的改变,从而求出系统重力势能的改变量;
(2)根据两球转动的角速度相同可求得速度关系,再根据机械能守恒定律列式即可求得AB的速度;
(3)对A球分析,根据向心力公式即可求得杆对球的作用力,从而求出球对杆的作用力.
解答 解:(1)A球下降高度为2L,故重力势能减小了△EPA=2mgL;
B球升高的高度为L,故重力势能增加了△EPB=mgL;
系统的重力势能减小量为:△EP=2mgL-mgL=mgL;
(2)在转动中两球的机械能守恒,同时两球转动的角速度相同,根据v=ωr可知,vA=2vB;
根据机械能守恒定律可知:
△EP=$\frac{1}{2}$mvA2+$\frac{1}{2}$mvB2;
联立解得:vA=2$\sqrt{\frac{2gL}{5}}$;vB=$\sqrt{\frac{2gL}{5}}$;
(3)对A球分析可知,A球受到的重力和杆的拉力充当向心力,则有:
mg+F=m$\frac{{v}_{A}^{2}}{2L}$
解得:F=-$\frac{1}{5}$mgL,负号说明杆提供支持力,方向向上;
则由牛顿第三定律可知,A对杆的拉力为$\frac{1}{5}$mgL,
答:(1)A球的重力势能减小2mgL;B球的重力势能增加mgL;系统的重力势能减小mgL;
(2)转到竖直位置时A、B两球的速度为2$\sqrt{\frac{2gL}{5}}$和$\sqrt{\frac{2gL}{5}}$;
(3)A球对细杆的拉力为$\frac{1}{5}$mgL
点评 本题考查机械能守恒定律的应用,要注意明确两球在转动中没有重力之外的其他力做功,总机械能守恒;同时要注意明确两球转动时两球的角速度相同,从而明确线速度间的大小关系.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案 如图所示,在光滑绝缘的水平面上方,有两个方向相反的水平方向匀强磁场,PQ为两个磁场的边界,磁场范围足够大,磁感应强度的大小分别为B1=B、B2=2B.一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框,以速度v垂直磁场方向从图中实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列结论中正确的是( )
如图所示,在光滑绝缘的水平面上方,有两个方向相反的水平方向匀强磁场,PQ为两个磁场的边界,磁场范围足够大,磁感应强度的大小分别为B1=B、B2=2B.一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框,以速度v垂直磁场方向从图中实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列结论中正确的是( )| A. | 此过程中通过线框截面的电量为$\frac{B{a}^{2}}{2R}$ | |
| B. | 此过程中回路产生的电能为$\frac{3m{v}^{2}}{8}$ | |
| C. | 此时线框的加速度为$\frac{9{B}^{2}{a}^{2}v}{2mR}$ | |
| D. | 此时线框中的电功率为$\frac{9{B}^{2}{a}^{2}{v}^{2}}{2R}$ |
| A. | 三个小球都做变加速运动 | |
| B. | 三个小球都做匀变速运动 | |
| C. | 斜向上抛出的小球在最高点时的速度为0 | |
| D. | 斜向下抛出的小球落地时的速度方向可能竖直向下 |
 如图中,摆球A、B用细线悬挂在天花板上,两球刚好接触,现将摆球A在两摆线所在平面内向左拉开一小角度后释放,碰撞后,两摆球分开各自做简谐运动,以mA、mB分别表示A、B摆球的质量,则( )
如图中,摆球A、B用细线悬挂在天花板上,两球刚好接触,现将摆球A在两摆线所在平面内向左拉开一小角度后释放,碰撞后,两摆球分开各自做简谐运动,以mA、mB分别表示A、B摆球的质量,则( )| A. | 如果mA>mB,下一次碰撞将发生在平衡位置右侧 | |
| B. | 如果mA<mB,下一次碰撞将发生在平衡位置左侧 | |
| C. | 无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置 | |
| D. | 无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置左侧 |
 如图所示,水平地面上的木箱质量为20kg.用F=100N的水平力拉木箱,恰好能使木箱匀速前进,求:
如图所示,水平地面上的木箱质量为20kg.用F=100N的水平力拉木箱,恰好能使木箱匀速前进,求: