题目内容
3. 如图所示,在光滑绝缘的水平面上方,有两个方向相反的水平方向匀强磁场,PQ为两个磁场的边界,磁场范围足够大,磁感应强度的大小分别为B1=B、B2=2B.一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框,以速度v垂直磁场方向从图中实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列结论中正确的是( )
如图所示,在光滑绝缘的水平面上方,有两个方向相反的水平方向匀强磁场,PQ为两个磁场的边界,磁场范围足够大,磁感应强度的大小分别为B1=B、B2=2B.一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框,以速度v垂直磁场方向从图中实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列结论中正确的是( )| A. | 此过程中通过线框截面的电量为$\frac{B{a}^{2}}{2R}$ | |
| B. | 此过程中回路产生的电能为$\frac{3m{v}^{2}}{8}$ | |
| C. | 此时线框的加速度为$\frac{9{B}^{2}{a}^{2}v}{2mR}$ | |
| D. | 此时线框中的电功率为$\frac{9{B}^{2}{a}^{2}{v}^{2}}{2R}$ |
分析 根据法拉第电磁感应定律、欧姆定律和电量q=I△t相结合求解电量.此时线框中感应电动势为E=2Ba$•\frac{v}{2}$,感应电流为I=$\frac{E}{R}$,线框所受的安培力的合力为F=2BIa,再由牛顿第二定律求解加速度.根据能量守恒定律求解产生的电能.由P=I2R求解电功率.
解答 解:A、感应电动势为:E=$\frac{△Φ}{△t}$,其中△Φ=2B•$\frac{1}{2}{L}^{2}$+$B•\frac{1}{2}{L}^{2}$=$\frac{3}{2}B{L}^{2}$,感应电流为:I=$\frac{E}{R}$,电荷量为:q=I△t,解得:q=$\frac{3B{a}^{2}}{2R}$,故A错误.
B、由能量守恒定律得,此过程中回路产生的电能为:E=$\frac{1}{2}$mv2-$\frac{1}{2}m(\frac{v}{2})^{2}$=$\frac{3}{8}$mv2,故B正确;
C、此时感应电动势:E=(2Ba+Ba)$•\frac{v}{2}$=$\frac{3}{2}Bav$,线框电流为:I=$\frac{E}{R}=\frac{3Bav}{2R}$,由牛顿第二定律得:2BIa+BIa=ma加,解得:a加=$\frac{9{B}^{2}{a}^{2}v}{2mR}$,故C正确;
D、此时线框的电功率为:P=I2R=$\frac{9{B}^{2}{a}^{2}{v}^{2}}{4R}$,故D错误;
故选:BC.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

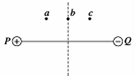 如图所示,P、Q是两个电荷量相等的异种电荷,在其电场中有a、b、c三点在一条直线上,平行于P、Q的连线,b在P、Q连线的中垂线上,ab=bc,下列说法正确的( )
如图所示,P、Q是两个电荷量相等的异种电荷,在其电场中有a、b、c三点在一条直线上,平行于P、Q的连线,b在P、Q连线的中垂线上,ab=bc,下列说法正确的( )| A. | 电场强度:Eb>Ea>Ec | B. | 电势:φa>φc>φb | ||
| C. | 电场强度:Ea>Eb>Ec | D. | 电势:φa>φb>φc |
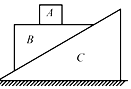 如图所示,物体B的上表面水平,当A、B相对静止沿斜面匀速下滑时,斜面保持静止不动,则下列判断正确的是( )
如图所示,物体B的上表面水平,当A、B相对静止沿斜面匀速下滑时,斜面保持静止不动,则下列判断正确的是( )| A. | 物体C受水平面的摩擦力为零 | |
| B. | 物体B的上表面一定是粗糙的 | |
| C. | 物体C受到5个力作用 | |
| D. | 水平面对物体C的支持力小于三物体的重力大小之和 |
 的力压弹簧的另一端,平衡时长度为
的力压弹簧的另一端,平衡时长度为 ;改用大小为
;改用大小为 的力拉弹簧,平衡时长度为
的力拉弹簧,平衡时长度为 。弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为
。弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为 B.
B. C.
C. D.
D.

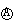 与一电阻R并联可制成一电流表,在检测新制成的电流表时,如果发现它的示数总比准确值稍微小一些或稍微大一些,那么应分别采取什么措施加以修正( )
与一电阻R并联可制成一电流表,在检测新制成的电流表时,如果发现它的示数总比准确值稍微小一些或稍微大一些,那么应分别采取什么措施加以修正( )
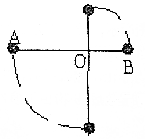 如图所示,一轻细杆两端分别固定着两只质址均为m的小球,O点为光滑水平轴,已知AO=2L,BO=L,轻杆水平时无初速释放小球至轻杆竖直位置过程中,不计空气阻力.
如图所示,一轻细杆两端分别固定着两只质址均为m的小球,O点为光滑水平轴,已知AO=2L,BO=L,轻杆水平时无初速释放小球至轻杆竖直位置过程中,不计空气阻力.