题目内容
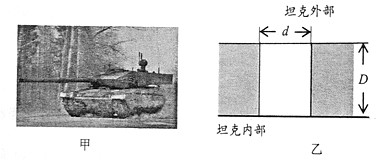
8.99式主战坦克是目前我国陆军装配先进的主战坦克(图甲).为了从坦克内部观察外界目标,坦克的前壁上开了一圆形观察孔,在孔中完全嵌入折射率为√3的特制光学玻璃,厚度和坦克壁厚度相同.如图乙(俯视)所示,假定该型号坦克的前壁装甲厚度为D=10√3cm,观察孔直径d=10cm,求:(1)光进入这块光学玻璃时的传播速度多大(光在空气中的速度取c=3.0×108m/s)?
(2)如果坦克内的人眼睛贴着这块玻璃观察外界,能看到的外界的角度范围为多大?
(3)要使坦克内的人眼睛贴着这块玻璃能看到的外界的角度接近180°,则嵌入的特制玻璃折射率应为多大?
分析 (1)根据公式v=cn求光进入这块光学玻璃时的传播速度.
(2)根据题意画出光路图,然后再利用几何关系求出最大的折射角,由折射定律即可求得最大的入射角,从而得到视角范围.
(3)要使坦克内的人眼睛贴着这块玻璃能看到的外界的角度接近180°,可知长方形孔的边缘的入射光线与法线成90°角,根据折射定律求折射率.
解答 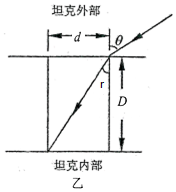 解:(1)光进入这块光学玻璃时的传播速度为 v=cn=3×108√3≈1.73×108m/s
解:(1)光进入这块光学玻璃时的传播速度为 v=cn=3×108√3≈1.73×108m/s
(2)人眼睛贴着这块玻璃左侧观察外界时的光路如图,由几何知识有:
sinr=d√d2+D2=10√102+(10√3)2=0.5,r=30°
由折射定律得:n=sinθsinr
故:sinθ=nsinr=√3×0.5=√32
得:θ=60°
因此坦克内的人通过这块玻璃能看到的外界的角度范围为:2θ=120°.
(3)要使坦克内的人眼睛贴着这块玻璃能看到的外界的角度接近180°,则有 θ=90°
则嵌入的特制玻璃折射率为 n′=sin90°sinr=2
答:
(1)光进入这块光学玻璃时的传播速度为1.73×108m/s.
(2)坦克内的人通过这块玻璃能看到的外界的角度范围为120°.
(3)嵌入的特制玻璃折射率为2.
点评 对于几何光学问题,正确画出光路图是解答的基础,同时要充分运用几何知识,帮助求解相关角度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.以下说法正确的是( )
| A. | 两个直线运动的合运动一定为直线运动 | |
| B. | 合运动的速度为各分运动速度大小之和 | |
| C. | 分运动与合运动的运动时间是相同的 | |
| D. | 两个匀变速直线运动的合运动一定为匀变速直线运动 |
3.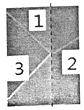 如图是一束白光从一种透明介质进入另一种透明介质的光路图,其中虚线是两种介质的分界线.下列说法正确的是( )
如图是一束白光从一种透明介质进入另一种透明介质的光路图,其中虚线是两种介质的分界线.下列说法正确的是( )
 如图是一束白光从一种透明介质进入另一种透明介质的光路图,其中虚线是两种介质的分界线.下列说法正确的是( )
如图是一束白光从一种透明介质进入另一种透明介质的光路图,其中虚线是两种介质的分界线.下列说法正确的是( )| A. | 光线1是入射光,光线2是反射光,光线3是折射光 | |
| B. | 光线2是入射光,光线1是反射光,光线3是折射光 | |
| C. | 光线3是入射光,光线1是反射光,光线2是折射光 | |
| D. | 改变入射光线的入射角,在界面上可能发生全反射 |
20.关于运动的合成与分解,下列说法正确的是( )
| A. | 合运动的速度一定大于两个分运动的速度 | |
| B. | 合运动的时间大于分运动的时间 | |
| C. | 两个分运动是直线运动,它们的合运动可能是曲线运动 | |
| D. | 两个分运动是匀速直线运动,它们的合运动可能是匀变速直线运动 |
3. 如图所示,水平桌面上叠放着A、B两物体,B物体受力F作用,A、B 一起相对地面向右做减速直线运动,则 B 物体的受力个数为( )
如图所示,水平桌面上叠放着A、B两物体,B物体受力F作用,A、B 一起相对地面向右做减速直线运动,则 B 物体的受力个数为( )
 如图所示,水平桌面上叠放着A、B两物体,B物体受力F作用,A、B 一起相对地面向右做减速直线运动,则 B 物体的受力个数为( )
如图所示,水平桌面上叠放着A、B两物体,B物体受力F作用,A、B 一起相对地面向右做减速直线运动,则 B 物体的受力个数为( )| A. | 4 个 | B. | 5 个 | C. | 6 个 | D. | 7 个 |
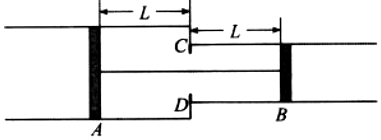
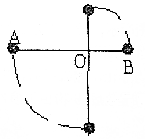 如图所示,一轻细杆两端分别固定着两只质址均为m的小球,O点为光滑水平轴,已知AO=2L,BO=L,轻杆水平时无初速释放小球至轻杆竖直位置过程中,不计空气阻力.
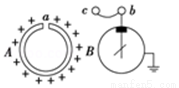
如图所示,一轻细杆两端分别固定着两只质址均为m的小球,O点为光滑水平轴,已知AO=2L,BO=L,轻杆水平时无初速释放小球至轻杆竖直位置过程中,不计空气阻力.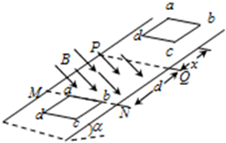 如图所示,倾角为α=30°的光滑固定斜面,斜面上相隔为d=8m平行虚线MN与PQ间有大小为B=0.1T的匀强磁场,方向垂直斜面向下.一质量为m=0.1kg,电阻为R=0.2Ω,边长L=1m的正方形单匝纯电阻金属线圈,线圈cd边从距PQ上方x=2.5m处由静止释放沿斜面下滑进入磁场,切ab边刚要离开磁场时线圈恰好做匀速运动,重力加速度g=10m/s2.求:
如图所示,倾角为α=30°的光滑固定斜面,斜面上相隔为d=8m平行虚线MN与PQ间有大小为B=0.1T的匀强磁场,方向垂直斜面向下.一质量为m=0.1kg,电阻为R=0.2Ω,边长L=1m的正方形单匝纯电阻金属线圈,线圈cd边从距PQ上方x=2.5m处由静止释放沿斜面下滑进入磁场,切ab边刚要离开磁场时线圈恰好做匀速运动,重力加速度g=10m/s2.求: