Question

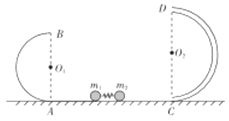
【题目】如图，在竖直平面内，一半径为的光滑半圆轨道和的光滑半圆筒轨道与水平光滑轨道AC在A、C点相切。质量为和的可视为质点的小球用一根细线相连，中间夹着一个被压缩的轻质弹簧，最初处于静止状态。将细线烧断，恰好可以通过B点，重力加速度大小为。求：

（1）小球被弹簧弹开的速度；

（2）判断小球能否上到D点，说明理由。若能上到最高点，求在最高点轨道对小球的作用力。

Answer 1

【答案】（1）；（2），方向竖直向上

【解析】

(1)在B点对小球受力分析，由牛顿第二定律得：

由A到B应用动能定理有：

代入数据解得

两个小球被弹开的过程中系统动量守恒，得：

代入数据解得

(2)假设可以上到D点，由动能定理得：

解得

由于是半圆筒轨道，能上到最高点的临界速度是零，所以经判断能上到最高点D，在D点对小球受力分析，取向下为正方向，由牛顿第二定律得：

代入数据解得

负号表示方向竖直向上，即大小为：.

答：(1)小球被弹簧弹开的速度；

(2)小球能上到最高点，在最高点轨道对小球的作用力大小为，方向竖直向上。