题目内容
4. 为了“探究外力做功与物体动能变化的关系”,某同学查资料得知,弹簧的弹力做功与形变量的关系为Ep=$\frac{1}{2}$kx2,其中k是弹簧的劲度系数,x是弹簧长度的变化量.
为了“探究外力做功与物体动能变化的关系”,某同学查资料得知,弹簧的弹力做功与形变量的关系为Ep=$\frac{1}{2}$kx2,其中k是弹簧的劲度系数,x是弹簧长度的变化量.该同学设计实验如下:
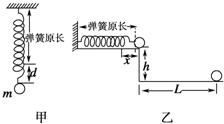
首先进行如图甲所示的实验:将轻质弹簧竖直挂起来,在弹簧的另一端挂上小铁球m,静止时测得弹簧的伸长量为d.
在此步骤中,目的是要确定物理量弹簧劲度系数k,用m、d、g表示为$\frac{mg}{d}$.
接着进行如图乙所示的实验:将这根弹簧放在光滑的水平桌面上,一端固定,另一端被小铁球压缩,测得压缩量为x,释放弹簧后,小铁球被推出去,从高为h的水平桌面上抛出,小铁球在空中运动的水平距离为L.则小铁球做平抛运动的初动能Ek0=$\frac{{mg{L^2}}}{4h}$.弹簧对小铁球做的功W=$\frac{{mg{x^2}}}{2d}$.(用m、x、d、g表示).对比W和Ek0的关系,就可以得出:在实验误差允许范围内,外力所做的功等于物体动能的变化.
分析 (1)甲所示实验的目的是测量弹簧的劲度系数k,由胡克定律得到k;
(2)乙图所示的乙实验:弹簧的弹性势能转化为小球的动能,利用平抛运动的规律求出平抛运动的初速度,小球O末动能Ek2=$\frac{1}{2}m{{v}_{0}}^{2}$.再根据功能关系求出弹簧对小球O做的功W=$\frac{1}{2}k{x}^{2}$.
解答 解:(1)该同学做甲图所示实验的目的是测量弹簧的劲度系数k,当小球静止时,有
mg=kd,可得k=$\frac{mg}{d}$.
(2)将弹簧压缩x后释放,小球O初动能Ek1=0;
小球离开桌面后,以初速度v0做平抛运动,则有
L=v0t,h=$\frac{1}{2}g{t}^{2}$
可得v0=L$\sqrt{\frac{g}{2h}}$
则小球O末动能Ek2=$\frac{1}{2}m{{v}_{0}}^{2}$=$\frac{1}{2}m(L\sqrt{\frac{g}{2h}})^{2}=\frac{mg{L}^{2}}{4h}$
根据功能关系得:弹簧对小球O做的功W=$\frac{1}{2}k{x}^{2}$=$\frac{1}{2}•\frac{mg}{d}•{x}^{2}$=$\frac{{mg{x^2}}}{2d}$.
故答案为:弹簧劲度系数k;$k=\frac{mg}{d}$;$\frac{{mg{L^2}}}{4h}$;$\frac{{mg{x^2}}}{2d}$
点评 本题借助于平抛运动以及胡克定律,考查探究外力做功与物体动能变化关系的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.在力学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是( )
| A. | 牛顿应用理想斜面实验总结出了牛顿第一定律 | |
| B. | 亚里士多德认为力的真正效应总是改变物体的速度,而不仅仅是使之运动 | |
| C. | 牛顿最早指出力不是维持物体运动的原因 | |
| D. | 胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 |
15. 一根不均匀直细棒,用两轻绳系于A、B两端,然后悬挂于O点,如图所示,静止时,OC为竖直方向,从图示情况可知( )
一根不均匀直细棒,用两轻绳系于A、B两端,然后悬挂于O点,如图所示,静止时,OC为竖直方向,从图示情况可知( )
 一根不均匀直细棒,用两轻绳系于A、B两端,然后悬挂于O点,如图所示,静止时,OC为竖直方向,从图示情况可知( )
一根不均匀直细棒,用两轻绳系于A、B两端,然后悬挂于O点,如图所示,静止时,OC为竖直方向,从图示情况可知( )| A. | 棒的重心位置在D点 | |
| B. | 棒的右端B比左端A粗 | |
| C. | AB两端细绳对A、B拉力的合力竖直向上 | |
| D. | O点对细绳的拉力沿DO方向斜向上 |
9.如图所示为一组电场线,A、B为其中两点,则( )


| A. | A点的场强小于B点的场强 | |
| B. | A点电势高于B点电势 | |
| C. | 将电子从A点移到B点,电场为做正功 | |
| D. | 正电荷在A点的电势能小于正电荷在B点的电势能 |
13. 如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )
如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )
 如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )
如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )| A. | 物体A受三个弹力作用 | B. | 物体A受两个弹力作用 | ||
| C. | 物体B受两个弹力作用 | D. | 物体A和物体B均只受一个弹力作用 |
 矩形线圈abcd,边长ab=30cm,bc=20cm,如图所示放在直角坐标内,α=30°,β=60°,设匀强磁场的磁感应强度B=10-2T,则
矩形线圈abcd,边长ab=30cm,bc=20cm,如图所示放在直角坐标内,α=30°,β=60°,设匀强磁场的磁感应强度B=10-2T,则  如图所示,一带电量数值为q的小球在悬线拉力作用下处于静止状态,此时悬线偏离竖直方向的夹角为θ,极板间距为d,则:
如图所示,一带电量数值为q的小球在悬线拉力作用下处于静止状态,此时悬线偏离竖直方向的夹角为θ,极板间距为d,则: