题目内容
如图所示,坐标系xOy位于竖直平面内,在该区域内有场强E=12N/C、方向沿x轴正方向的匀强电场和磁感应强度大小为B=2T、沿水平方向且垂直于xOy平面指向纸里的匀强磁场.一个质量m=4×10-5kg,电量q=2.5×10-5C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10m/s2,求:
(1)微粒运动到原点O时速度的大小和方向;
(2)P点到原点O的距离.
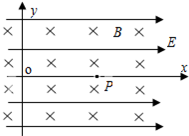
(1)微粒运动到原点O时速度的大小和方向;
(2)P点到原点O的距离.

(1)微粒运动到O点之前要受到重力、电场力和洛伦兹力作用,
在这段时间内微粒做匀速直线运动,说明三力合力为零.由此可得
 (Bqv)2=(qE)2+(mg)2,代入数据解得:v=10m/s,
(Bqv)2=(qE)2+(mg)2,代入数据解得:v=10m/s,
速度v与重力和电场力的合力的方向垂直.设速度v与x轴的夹角为θ,
则:tanθ=
,代入数据得:tanθ=
,即θ=37°;
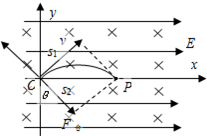
(2)微粒运动到O点后,撤去磁场,微粒只受到重力、电场力作用,
其合力为一恒力,且方向与微粒在O点的速度方向垂直,所以微粒做类平抛运动,
可沿初速度方向和合力方向进行分解.
设沿初速度方向的位移为s1,沿合力方向的位移为s2,
在初速度方向上:s1=vt,
在合力方向上:s2=
t2,
OP间的距离:OP=
联立解得P点到原点O的距离:OP=15m;
答:(1)粒子运动的速度大小为10m/s,方向与x轴夹角为37度;
(2)P点到原点O的距离为15m.
在这段时间内微粒做匀速直线运动,说明三力合力为零.由此可得
 (Bqv)2=(qE)2+(mg)2,代入数据解得:v=10m/s,
(Bqv)2=(qE)2+(mg)2,代入数据解得:v=10m/s,速度v与重力和电场力的合力的方向垂直.设速度v与x轴的夹角为θ,
则:tanθ=
| FE |
| mg |
| 3 |
| 4 |
(2)微粒运动到O点后,撤去磁场,微粒只受到重力、电场力作用,
其合力为一恒力,且方向与微粒在O点的速度方向垂直,所以微粒做类平抛运动,
可沿初速度方向和合力方向进行分解.
设沿初速度方向的位移为s1,沿合力方向的位移为s2,
在初速度方向上:s1=vt,
在合力方向上:s2=
| 1 |
| 2 |
| ||
| m |
OP间的距离:OP=
| s1 |
| cosθ |
联立解得P点到原点O的距离:OP=15m;
答:(1)粒子运动的速度大小为10m/s,方向与x轴夹角为37度;
(2)P点到原点O的距离为15m.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目