题目内容
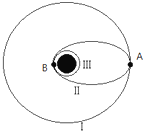
如图所示,a、b、c、d是在地球大气层外的圆形轨道上匀速运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于c卫星的正上方.下列说法中正确的是( )

| A.b、d存在相撞危险 |
| B.a、c的加速度大小相等,且大于b的加速度 |
| C.b、c的角速度大小相等,且小于a的角速度? |
| D.a、c的线速度大小相等,且小于d的线速度? |

A、人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有
F=F向
F=G
F向=m
=mω2r=m(
)2r
因而
G
=m
=mω2r=m(
)2r=ma
解得
v=
①
ω=
=
②
a=
③
b、d两颗卫星的轨道半径相同,根据①式,它们的线速度相等,故永远不会相撞,故A错误;
B、a、c两颗卫星的轨道半径相同,且小于b卫星的轨道半径,根据③式,a、c的加速度大小相等,且大于b的加速度,故B正确;
C、b、c两颗卫星的轨道半径不相同,根据②式,其角速度不等,故C错误;
D、a、c两颗卫星的轨道半径相同,且小于d卫星的轨道半径,根据①式,a、c的线速度大小相等,且大于d的线速度,故D错误;
故选B.
F=F向
F=G
| Mm |
| r2 |
F向=m
| v2 |
| r |
| 2π |
| T |
因而
G
| Mm |
| r2 |
| v2 |
| r |
| 2π |
| T |
解得
v=
|
ω=
| v |
| r |
|
a=
| GM |
| r2 |
b、d两颗卫星的轨道半径相同,根据①式,它们的线速度相等,故永远不会相撞,故A错误;
B、a、c两颗卫星的轨道半径相同,且小于b卫星的轨道半径,根据③式,a、c的加速度大小相等,且大于b的加速度,故B正确;
C、b、c两颗卫星的轨道半径不相同,根据②式,其角速度不等,故C错误;
D、a、c两颗卫星的轨道半径相同,且小于d卫星的轨道半径,根据①式,a、c的线速度大小相等,且大于d的线速度,故D错误;
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目