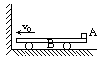
题目内容
两个小球1和2的质量分别是m1=2.0kg，m2=1.6kg，球1静止于光滑的水平面上的A点，球2在水平面上从远处沿两球心连线向着1球运动。假设两球相距L≤18m时存在着恒定的斥力F，L>18m时无相互作用力。当两球相距最近时，它们的距离为d=2.0m，球2的速度为v=4m/s。求：
（1）两球间的斥力的大小。
（2）球1速度达最大时距A点的最小距离S。
（1）两球间的斥力的大小。
（2）球1速度达最大时距A点的最小距离S。
（1）F=2.25N
（2）28.4m
（2）28.4m
（1）设最近时速度均为V，1、2两球发生的位移分别为S1、S2，由动量守恒定律得：
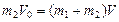
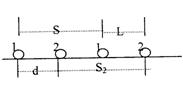
由动能定理得：
FS1=m2V2/2
几何关系得：S1+L=S2+S
联立以上四式得：V0="9m/s " F="2.25N "
（说明：其他方法也可。）
（2）设球1达最大速度为V1，这时球2速度为V2，球1、2的位移分别为S1、S2，球1速度达到最大时二者间距恢复为L，由动量守恒得：
m2V0=m1V1+m2V2
由动能定理有：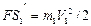
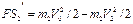
几何关系得：S1′=S2′
联立以上四式得：S1′="28.4m " V1="8.0m/s "
（说明：其他方法也可。）
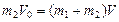
由动能定理得：
FS1=m2V2/2
几何关系得：S1+L=S2+S
联立以上四式得：V0="9m/s " F="2.25N "
（说明：其他方法也可。）
（2）设球1达最大速度为V1，这时球2速度为V2，球1、2的位移分别为S1、S2，球1速度达到最大时二者间距恢复为L，由动量守恒得：
m2V0=m1V1+m2V2
由动能定理有：
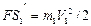
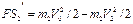
几何关系得：S1′=S2′
联立以上四式得：S1′="28.4m " V1="8.0m/s "
（说明：其他方法也可。）
练习册系列答案
阅读快车系列答案
相关题目
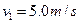和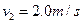
同时冲上小车，当它们相对于小车停止滑动时，没有相碰。已知Ａ、Ｂ两物体与车面的动摩擦因数都是0.20，取ｇ＝10
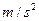，求：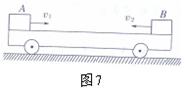
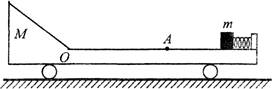
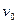击中木块A并留在其中，子弹打入木块的过程持续时间极短，可
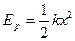.如果此后运动过程中弹簧始终处于弹性限度内，且A、B不会发生直接碰触。试求：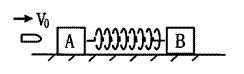
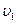开始向右运动。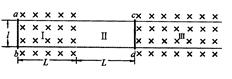
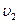，求ab棒通过区域II的时间；
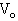与竖直墙壁相撞．若碰撞时间极短且无能量损失，撞后A恰好未从B上落下来，A与B间的动摩擦因数为μ.