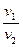题目内容
如图所示,光滑水平面上有一长板车,车的上表面0A段是一长为己的水平粗 糙轨道,A的右侧光滑,水平轨道左侧是一光滑斜面轨道,斜面轨道与水平轨道在O点平 滑连接。车右端固定一个处于锁定状态的压缩轻弹簧,其弹性势能为Ep,一质量为m的小物体(可视为质点)紧靠弹簧,小物体与粗糙水平轨道间的动摩擦因数为μ,整个装置处于静止状态。现将轻弹簧解除锁定,小物体被弹出后滑上水平粗糙轨道。车的质量为 2m,斜面轨道的长度足够长,忽略小物体运动经过O点处产生的机械能损失,不计空气阻力。求:
(1)解除锁定结束后小物体获得的最大动能;
(2)当μ满足什么条件小物体能滑到斜面轨道上,满足此条件时小物体能上升的最大高度为多少?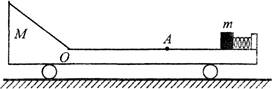
(1)解除锁定结束后小物体获得的最大动能;
(2)当μ满足什么条件小物体能滑到斜面轨道上,满足此条件时小物体能上升的最大高度为多少?

(1)
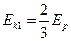 (2)
(2)
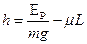
(1)设解锁弹开后小物体的最大速度饷大小为v1,小物体的最大动啦为Ek ,此时长板车的速度大小为v2,研究解锁弹开过程小物体和车组成的系统,根据动量守恒和机械能守恒,有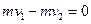 ①(2分)
①(2分)
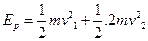 ②(3分)
②(3分)
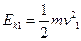 ③(1分)
③(1分)
联立①②③式解得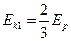 ④(2分)
④(2分)
(2)小物体相对车静止时,二者有共同的速度设为V共,长板车和小物体组成的系统水平方向动量守恒 ⑤(2分)
⑤(2分)
所以v共="0 " ⑥(1分)
要使小物体能滑上斜面轨道,:必须满足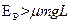 ;⑦( 3分)
;⑦( 3分)
即当 时,小物体能滑上斜面轨道⑧ (1分)
时,小物体能滑上斜面轨道⑧ (1分)
设小物体上升的最大高度为h,此瞬间小物体相对车静止,由⑤式知两者有共同速度为零.⑨(1分)
根据系统能量守恒有
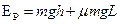 ⑩(3分)
⑩(3分)
解得: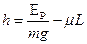 (1分)
(1分)
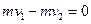 ①(2分)
①(2分)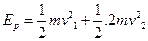 ②(3分)
②(3分)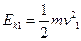 ③(1分)
③(1分)联立①②③式解得
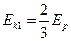 ④(2分)
④(2分)(2)小物体相对车静止时,二者有共同的速度设为V共,长板车和小物体组成的系统水平方向动量守恒
 ⑤(2分)
⑤(2分)所以v共="0 " ⑥(1分)
要使小物体能滑上斜面轨道,:必须满足
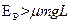 ;⑦( 3分)
;⑦( 3分)即当
 时,小物体能滑上斜面轨道⑧ (1分)
时,小物体能滑上斜面轨道⑧ (1分)设小物体上升的最大高度为h,此瞬间小物体相对车静止,由⑤式知两者有共同速度为零.⑨(1分)
根据系统能量守恒有
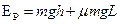 ⑩(3分)
⑩(3分) 解得:
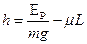 (1分)
(1分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

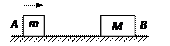

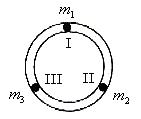
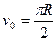 沿槽运动,R为圆环的内半径和小球半径之和,各球之间的碰撞皆为弹性碰撞,求此系统的运动周期T。
沿槽运动,R为圆环的内半径和小球半径之和,各球之间的碰撞皆为弹性碰撞,求此系统的运动周期T。