Question

【题目】如图甲所示，质量M=0.8kg的足够长的木板静止在光滑的水平面上，质量m=0.2kg的滑块静止在木板的左端，在滑块上施加一水平向右、大小按图乙所示随时间变化的拉力F，4s后撤去力F。若滑块与木板间的动摩擦因数，最大静摩擦力等于滑动摩擦力，重力加速度g=10m/s2,则下列说法正确的是（ ）

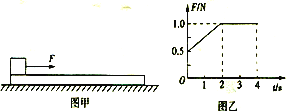
A. 0~4s时间内拉力的冲量共为3.2N·s

B. t=4s时滑块的速度大小为9.5m/s

C. 木板受到滑动摩擦力的冲量共为2.8N·s

D. 木板的速度最大为2m/s

Answer 1

【答案】BC

【解析】A、拉力F的冲量等于F-t图像的面积，0~4s时间内拉力的冲量I= ，A错误；

B、滑块与木板间恰好打滑时，对木板: .

对滑块:

解得F0=0.5N，a0=0.5m/s2.

所以t=0时刻，A.B恰好开始打滑

对滑块:IFμmgt=mv1，解得4s末滑块的速度v1=9.5m/s，B正确；

C、t=4s时，木板的速度v2=a0t=0.5×4=2m/s，

之后A加速，B减速，直到共速。取向右为正方向，由动量守恒定律得：

mv1+Mv2=(m+M)v

解得木板的最大速度v=3.5m/s

对木板:由动量定理得I=Mv

解得I=2.8Ns，C正确，D错误；

故选：BC。