题目内容
【题目】如图在光滑水平面上,视为质点、质量均为m=1㎏的小球a、b相距d=3m , 若b球处于静止,a球以初速度v0=4m/s , 沿ab连线向b球方向运动,假设a、b两球之间存在着相互作用的斥力,大小恒为F=2N , 从b球运动开始,解答下列问题: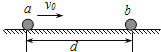
(1)通过计算判断a、b两球能否发生撞击.
(2)若不能相撞,求出a、b两球组成的系统机械能的最大损失量.
(3)若两球间距足够大,b球从开始运动到a球速度为零的过程,恒力F对b球做的功.
【答案】
(1)
假设没有相撞,二者同速时间距最小,由于系统动量守恒,以a的初速度方向为正方向,由动量守恒得:mv0=2mv,代入数据解得:v=2m/s,
由动能定理得:对a球:-FSa= ![]() -
- ![]() ,
,
代入数据解得:sa=3m,
对b球:FSb= ![]() ,代入数据解得:sb=1m,
,代入数据解得:sb=1m,
sa﹣sb=2m<d=3m,假设两球没有相撞成立
(2)
两球同速时机械能损失量最大,
由能量守恒定律得:△EK= ![]() mv02﹣
mv02﹣ ![]() 2mv2,
2mv2,
代入数据解得:△EK=4J
(3)
当a球速度为零时,以a的初速度方向为正方向,
由动量守恒得:mv0=mvb,代入数据解得:vb=4m/s,
由动能定理得,恒力F对b球做的功:
E= ![]() mvb2,代入数据解得:W=8J
mvb2,代入数据解得:W=8J
【解析】(1)两球组成的系统动量守恒,应用动量守恒定律与动能定理分析答题.(2)由能量守恒定律可以求出损失的机械能.(3)由动量守恒定律与动能定理可以求出功.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目