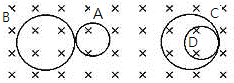题目内容
【题目】如图所示,在直角坐标系的原点O处有放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右边有一很薄的挡板,挡板的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m,带电荷量为q,速度为v,MN的长度为L,不计粒子重力。
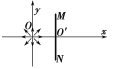
(1)若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度E0的最小值为多大?在电场强度E0取最小值时,打到板上的粒子动能为多大?
(2)若在整个空间加一方向垂直纸面向里的匀强磁场,要使整个挡板右侧都有粒子打到,磁场的磁感应强度不能超过多少(用m、v、q、L表示)?若满足此条件,放射源O向外发射出的所有带电粒子中有几分之几能打在板的左边?
【答案】(1) ![]()
![]() mv2 (2)
mv2 (2) ![]()
![]()
【解析】(1)由题意知,要使y轴右侧所有运动的粒子都能打在MN板上,其临界条件为:沿y轴方向运动的粒子做类平抛运动,且落在M或N点,则MO′=![]() L=vt①
L=vt①
a=![]() ②
②
OO′=![]() L=
L=![]() at2③
at2③
联立①②③式得E0=![]() ④
④
由动能定理知qE0×![]() L=Ek-
L=Ek-![]() mv2⑤
mv2⑤
联立④⑤式得Ek=![]() mv2⑥
mv2⑥
(2)由题意知,要使整个挡板右侧都有粒子打到,画出粒子的运动轨迹如图甲所示,分析知轨迹直径的最小值为MN板的长度L,则R0=![]() L=
L=![]() ⑦
⑦
甲
得B0=![]() ⑧
⑧
放射源O发射出的粒子中,打在MN板左侧的粒子的临界轨迹如图乙所示。

乙
因为OM=ON,且OM⊥ON
所以OO1⊥OO2
则v1⊥v2
故放射源O放射出的所有粒子中只有![]() 打在MN板的左侧。
打在MN板的左侧。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目