题目内容
16.一列火车从车站由静止开出做匀加速直线运动时,值班员站在第一节车厢前端的旁边,第一节车厢经过他历时3s,整个列车经过他历时12s,设各节车厢等长,车厢连接处的长度不计,求:(1)这列火车共有多少节车厢?
(2)最后七节车厢经过他身旁历时多少?
分析 换参考系,以火车为参照物,值班员做的是初速度为零的匀加速直线运动,(1)$x={v}_{0}t+\frac{1}{2}a{t}^{2}$对第一节通过和所有车厢通过,列出两个等式,联立即可求出,(1)再对除最后七节车厢列出关系式,与第一节通过的等式联立求解,然后用总时间减去即可得.
解答 解:每节车厢的长为L,共由N节,加速度为a
(1)第一节车厢通过:$L=\frac{1}{2}a{t}_{1}^{2}$
$L=\frac{1}{2}a×{3}^{2}$①
N节车厢通过:$NL=\frac{1}{2}a{t}^{2}$
$NL=\frac{1}{2}a{×12}^{2}$②
联立①②解得:N=16
(2)前九节车厢通过:$9L=\frac{1}{2}a{t}_{9}^{2}$③
联立①③解得:t9=9s
最后七节车厢经过他身旁历时△t=t-t9=3s
答:(1)这列火车共有16节车厢;
(2)最后七节车厢经过他身旁历时3s.
点评 考查转换参考系和对匀变速直线运动的基本公式,单个过程可以放到整个过程中去考虑,间接求解,容易求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.一带电体靠近一接地的空腔导体,空腔内无带电体,在静电平衡后下列物理量中等于零的有( )
| A. | 导体空腔内的电场强度 | B. | 导体外壳的带电量 | ||
| C. | 导体空腔内表面的带电量 | D. | 导体空腔内的电场线条数 |
7.理想变压器连接电路如图甲所示,当输入电压波形如图乙时,已知原副线圈的匝数比为10:1,电流表读数为2A,则( )


| A. | 电压表读数为282 V | B. | 电压表读数为28.2 V | ||
| C. | 输入功率为56.4 W | D. | 输入功率为40 W |
11.物体受到几个恒力的作用而处于平衡状态,若再对物体施加一个恒力,则物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | ||
| C. | 非匀变速曲线运动 | D. | 匀变速曲线运动 |
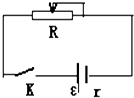 如图所示,电源电动势为E=6V,内电阻为r=1Ω,滑动变阻器电阻的阻值范围0-10Ω,当滑动变阻器电阻R=2Ω时,当 K闭合后,
如图所示,电源电动势为E=6V,内电阻为r=1Ω,滑动变阻器电阻的阻值范围0-10Ω,当滑动变阻器电阻R=2Ω时,当 K闭合后,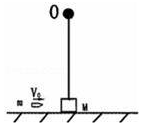 如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.
如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.