题目内容
1.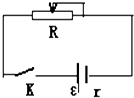 如图所示,电源电动势为E=6V,内电阻为r=1Ω,滑动变阻器电阻的阻值范围0-10Ω,当滑动变阻器电阻R=2Ω时,当 K闭合后,
如图所示,电源电动势为E=6V,内电阻为r=1Ω,滑动变阻器电阻的阻值范围0-10Ω,当滑动变阻器电阻R=2Ω时,当 K闭合后,求:(1)电路中的电流为多大?
(2)电路中路端电压为多少?
(3)电源的输出功率为多少?
(4)电源的总功率为多少?
分析 根据闭合电路欧姆定律列式求解电流;根据U=IR求解路端电压;根据P=UI求解电源的输出功率;根据P=EI求解求解电源的总功率.
解答 解:(1)根据闭合电路欧姆定律,电流:I=$\frac{E}{R+r}=\frac{6}{2+1}=2A$;
(2)电路中路端电压:U=IR=2×2V=4V;
(3)电源的输出功率为:P=UI=4V×2A=8W;
(4)电源的总功率为:P=EI=6V×2A=12W;
答:(1)电路中的电流为2A;
(2)电路中路端电压为4V;
(3)电源的输出功率为8W;
(4)电源的总功率为12W.
点评 本题关键是结合闭合电路欧姆定律列式求解电流,会根据欧姆定律求解内电压与外电压,知道电路中的能量转化情况,基础题目.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
11.一质量为m的小球沿倾角为θ的足够长的光滑斜面由静止开始滚下,途中依次经过A、B、C三点,已知AB=BC=ρ,由A到B和B到C经历的时间分别为t1=4s,t2=2s,则下列说法正确的是( )
| A. | 小球的加速度大小为$\frac{ρ}{3}$ | |
| B. | 小球经过B点重力的瞬时功率为$\frac{5mgρ}{12}$ | |
| C. | A点与出发点的距离为$\frac{ρ}{24}$ | |
| D. | 小球由静止到C点过程中重力的平均功率为$\frac{7mgρsinθ}{12}$ |
12.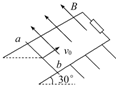 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )| A. | 向上滑行的时间大于向下滑行的时间 | |
| B. | 在向上滑行时电阻R上产生的热量小于向下滑行时电阻R上产生的热量 | |
| C. | 向上滑行时与向下滑行时通过电阻R的电荷量相等 | |
| D. | 金属杆从开始上滑至返回出发点,电阻R上产生的热量为$\frac{1}{2}$m(v02-v2) |
9.关于放射性元素,下列说法正确的是( )
| A. | 利用放射性同位素可作为示踪原子 | |
| B. | 利用放射性同位素放出的α射线可以进行金属探伤 | |
| C. | 放射性元素发生一次β衰变,质子数减少1 | |
| D. | 放射性元素的半衰期随环境温度的升高而缩短 |
6. 如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )
 如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )| A. | G | B. | Gsin θ | C. | Gcos θ | D. | Gtan θ |
13.在匀强磁场中,一矩形金属线框绕与磁感线垂直的转动轴匀速转动,如图甲所示.产生的交变电动势随时间变化的规律如图乙所示.则下列说法正确的是( )


| A. | t=0.01s时穿过线框的磁通量最大 | |
| B. | 该交变电动势的有效值为11$\sqrt{2}$V | |
| C. | 该交变电动势的瞬时值表达式为e=22$\sqrt{2}$sinV | |
| D. | 电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
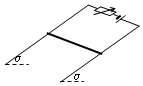 如图所示,光滑导轨与水平面成α角,导轨宽L,匀强磁场磁感应强度为B,金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求:
如图所示,光滑导轨与水平面成α角,导轨宽L,匀强磁场磁感应强度为B,金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求: 如图所示,带电小球A和B放在倾角为30°的光滑绝缘斜面上,质量均为m,所带电荷量分别为+q和-q,沿斜面向上的恒力F作用于A球,可使A、B保持间距r不变沿斜面向上加速运动,已知重力加速度为g,静电力常量k,求:
如图所示,带电小球A和B放在倾角为30°的光滑绝缘斜面上,质量均为m,所带电荷量分别为+q和-q,沿斜面向上的恒力F作用于A球,可使A、B保持间距r不变沿斜面向上加速运动,已知重力加速度为g,静电力常量k,求: