题目内容
5.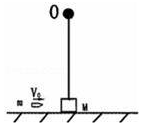 如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.
如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.
分析 要使木块能绕O点在竖直平面内做圆周运动,应用牛顿第二定律求出木块在最高点的临界速度,在木块从水平面到达最高点的过程中,机械能守恒,由机械能守恒定律可以求出木块在最低点的速度,根据动量守恒求出最小速度.
解答 解:当木块恰好能绕O点在竖直平面内做圆周运动时,在最高点重力提供向心力,由牛顿第二定律得:
(M+m)g=(M+m)$\frac{{v}_{1}^{2}}{L}$
代入数据解得:v1=2m/s,
从最低点到最高点过程系统机械能守恒,由机械能守恒得:
$\frac{1}{2}$(M+m)v2=$\frac{1}{2}$(M+m)v12+(M+m)g•2L
代入数据解得:v=2$\sqrt{5}$m/s
子弹射入木块过程系统动量守恒,以向右为正方向,由动量守恒定律得:
mv0=(M+m)v
代入数据解得:v0=80$\sqrt{5}$m/s;
答:子弹射入的最小速度为80$\sqrt{5}$m/s.
点评 本题考查了动量守恒定律的应用,分析清楚运动过程是正确解题的关键,应用牛顿第二定律、机械能守恒定律与动量守恒定律可以解题,解题时注意圆周运动临界条件的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在匀强磁场中,一矩形金属线框绕与磁感线垂直的转动轴匀速转动,如图甲所示.产生的交变电动势随时间变化的规律如图乙所示.则下列说法正确的是( )


| A. | t=0.01s时穿过线框的磁通量最大 | |
| B. | 该交变电动势的有效值为11$\sqrt{2}$V | |
| C. | 该交变电动势的瞬时值表达式为e=22$\sqrt{2}$sinV | |
| D. | 电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
17.一个质点做变速直线运动的v-t图象如图所示,下列说法中正确的是( )


| A. | 第1 s内与第5 s内的速度方向相同 | |
| B. | 第1 s内的加速度大小大于第5 s内的加速度 | |
| C. | OA、AB、BC段的加速度大小关系是aBC>aOA>aAB | |
| D. | OA段的加速度与速度方向相同,BC段的加速度与速度方向相反 |
14.一个物体做变速直线运动,物体的加速度从某一值逐渐减小到零.则在此过程中,关于该物体的运动情况,下列可能的是( )
| A. | 物体速度不断增大,加速度减小到零时,物体速度最大 | |
| B. | 物体速度不断减小,加速度减小到零时,物体速度为零 | |
| C. | 物体速度不断减小到零,然后物体反向做加速直线运动 | |
| D. | 物体先做匀减速直线运动,然后物体反向做匀加速直线运动 |
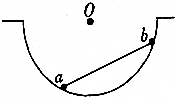 两个可视为质点的小球a和b,用质量可忽略不计、长度l=$\sqrt{2}$m的刚性细杆相连,放置在一个半径R=1m光滑的半球面内,如图所示.已知小球a的质量ma=2kg,小球b的质量mb=1kg.重力加速度g=10m/s2.求两小球平衡时细杆受到的压力大小.
两个可视为质点的小球a和b,用质量可忽略不计、长度l=$\sqrt{2}$m的刚性细杆相连,放置在一个半径R=1m光滑的半球面内,如图所示.已知小球a的质量ma=2kg,小球b的质量mb=1kg.重力加速度g=10m/s2.求两小球平衡时细杆受到的压力大小.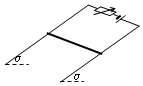 如图所示,光滑导轨与水平面成α角,导轨宽L,匀强磁场磁感应强度为B,金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求:
如图所示,光滑导轨与水平面成α角,导轨宽L,匀强磁场磁感应强度为B,金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求: