题目内容
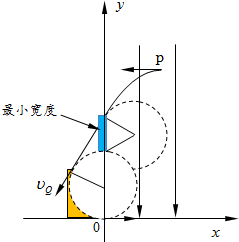
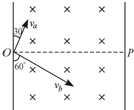
如图，一束电荷量为e的电子以垂直于磁感应强度B并垂直于磁场边界的速度v射入宽度为d的匀强磁场中，穿出磁场时速度方向θ=60°，求：
（1）穿越磁场的轨道半径；
（2）电子的质量；
（3）穿越磁场的时间；
（4）欲使电子从右边界射出，其速度v必须满足什么条件？
（1）穿越磁场的轨道半径；
（2）电子的质量；
（3）穿越磁场的时间；
（4）欲使电子从右边界射出，其速度v必须满足什么条件？
（1）粒子的运动轨迹图如图所示，根据几何关系有：r=
=
d；
（2）电子在磁场中做匀速圆周运动，由牛顿第二定律得：evB=m
，
解得：m=
；
（3）电子做圆周运动的周期：T=
=
，
所以电子穿越磁场的时间：t=
T=
×
=
．
（4）当电子与磁场右侧边界相切时，电子恰好不从磁场穿出，
此时电子轨道半径r=d，由牛顿第二定律得：evminB=m
，
解得：vmin=
v，
欲使电子从右边界射出，速度应大于
v；
答：（1）穿越磁场的轨道半径为
d；
（2）电子的质量
；
（3）穿越磁场的时间
；
（4）欲使电子从右边界射出，其速度最小为
v．
| d |
| sin60° |
2
| ||
| 3 |
（2）电子在磁场中做匀速圆周运动，由牛顿第二定律得：evB=m
| v2 |
| r |
解得：m=
2
| ||
| 3v |
（3）电子做圆周运动的周期：T=
| 2πr |
| v |
4
| ||
| 3v |
所以电子穿越磁场的时间：t=
| θ |
| 360° |
| 60° |
| 360° |
4
| ||
| 3v |
2
| ||
| 9v |
（4）当电子与磁场右侧边界相切时，电子恰好不从磁场穿出，
此时电子轨道半径r=d，由牛顿第二定律得：evminB=m
| ||
| r |
解得：vmin=
| ||
| 2 |
欲使电子从右边界射出，速度应大于
| ||
| 2 |
答：（1）穿越磁场的轨道半径为
2
| ||
| 3 |
（2）电子的质量
2
| ||
| 3v |
（3）穿越磁场的时间
2
| ||
| 9v |
（4）欲使电子从右边界射出，其速度最小为
| ||
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
