题目内容
【题目】如图所示，有一质量为M=2kg 的平板小车静止在光滑的水平地面上，现有质量均为m=1kg 的小物块A和B（均可视为质点），由车上P处开始，A以初速度v1=2m/s向左运动，B同时以v2=4m/s 向右运动．最终A、B两物块恰好停在小车两端没有脱离小车．两物块与小车间的动摩擦因数都为μ=0.1，取g=10m/s2 ． 求：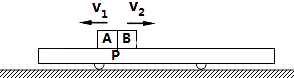
（1）求小车总长L；
（2）B在小车上滑动的过程中产生的热量QB；
（3）从A、B开始运动计时，经6s小车离原位置的距离x．
【答案】
（1）解：设最后达到共同速度v，整个系统动量守恒，以向右为正方向，由动量守恒定律得：
mv2﹣mv1=（2m+M）v﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
由能量守恒定律得：
μmgL= 
mv12+ mv22﹣ （2m+M）v2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
解得：v=0.5m/s，L=9.5m；
答：小车总长L为9.5m；
（2）解：A车离左端距离x1 刚运动到左端历时t1，在A运动至左端前，小车静止．
由牛顿第二定律得：μmg=maA﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣③
速度：v1=aAt1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣④
位移：x1= aAt12﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑤
解得：t1=2s，x1=2m，
所以，B离右端距离：x2=L﹣x1=7.5m，
热量：QB=μmgx2=7.5J；
答：B在小车上滑动的过程中产生的热量QB为7.5J；
（3）解：从开始到达到共速历时t2，
速度：v=v2﹣aBt2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑥
由牛顿第二定律得：μmg=maB﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑦
解得：t2=3.5s，
小车在t1前静止，在t1至t2之间以a向右加速：
由牛顿第二定律得：μmg=（M+m）a﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑧
小车向右走位移：s= a（t2﹣t1）2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑨
接下去三个物体组成的系统以v 共同匀速运动了：s′=v（6s﹣t2） ⑩
联立以上式子，解得：小车在6s内向右走的总距离：x=s+s′=1.625m；
答：从A、B开始运动计时，经6s小车离原位置的距离x为1.625m．
【解析】（1）两个物块A、B和小车组成的系统动量守恒，根据动量守恒定律求出共同速度，根据功能关系列式求出此过程中B运动的位移，三段位移之和即为小车的长度；
（2）B在小车上滑动的过程中产生的热量等于B滑动过程中克服摩擦力做的功；
（3）小车和A在摩擦力作用下做加速运动，由牛顿运动定律可得小车运动的加速度，再根据运动学基本公式即可求解．
