题目内容
【题目】如图甲是某同学测量重力加速度的装置，他将质量均为M的两个重物用轻绳连接，放在光滑的轻质滑轮上，这时系统处于静止状态．该同学在左侧重物上附加一质量为m的小重物，这时，由于小重物m的重力作用而使系统做初速度为零的缓慢加速运动，该同学用某种办法测出系统运动的加速度并记录下来．完成一次试验后，换用不同质量的小重物，并多次重复实验，测出不同m时系统的加速度a并作好记录．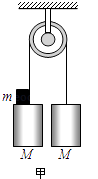
（1）若选定物块从静止开始下落的过程进行测量，则需要测量的物理量有
A.小重物的质量m
B.大重物的质量M
C.绳子的长度
D.重物下落的距离及下落这段距离所用的时间
（2）经过多次重复实验，得到多组a、m数据，作出 
﹣ 
图象，如图乙所示．已知该图象斜率为k，纵轴截距为b，则可求出当地的重力加速度g= ， 并可求出重物质量M= ． （用k和b表示）
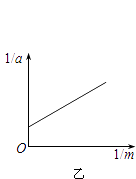
【答案】
（1）A,D
（2）
,
【解析】解：（1）对整体分析，根据牛顿第二定律得，mg=（2M+m）a，
解得a= 
根据h= 
at2，
g= 
所以需要测量的物理量有：小重物的质量m，重物下落的距离及下落这段距离所用的时间．故AD正确．
故选：AD．（2）因为a= ，
则 
= 
+ 
，
知图线斜率k= ，b= ，
解得g= ，M= ．
所以答案是：（1）AD；
练习册系列答案
相关题目
