题目内容
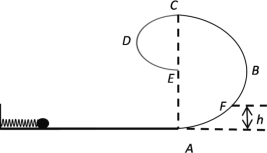
【题目】游乐场投掷游戏的简化装置如图所示，质量为2kg的球a放在高度h=1.8m的平台上，长木板c放在水平地面上，带凹槽的容器b放在c的最左端。a、b可视为质点，b、c质量均为1kg，b、c间的动摩擦因数μ1=0.4，c与地面间的动摩擦因数μ2=0.6.在某次投掷中，球a以v0=6m/s的速度水平抛出，同时给木板c施加一水平向左、大小为24N的恒力，使球a恰好落入b的凹槽内并瞬间与b合为一体。取g=10m/s2，求：
(1)球a抛出时，凹槽b与球a之间的水平距离x0；
(2)a、b合为一体时的速度大小；
(3)要使ab不脱离木板c，木板长度L的最小值。
【答案】(1)4.32m ；(2)3.2m/s；(3)2.96m.
【解析】
(1)a球从抛出到落到b槽内的时间
此过程中a球的水平位移
设a、b、c的质量分别为2m、m、m；假设bc之间无相对滑动一起向左加速运动，则加速度
则bc之间要产生相对滑动，其中b的加速度为
在时间t内槽b的位移为
球a抛出时，凹槽b与球a之间的水平距离
；
(2)a落在槽b中时，槽b的速度
方向向左，设向右为正方向，则对ab系统由动量守恒定律：
解得
v2=3.2m/s
(3)当a做平抛运动的时间内，木板c的加速度
当球a落到槽b中时木板c的速度
此时槽b相对木板c向右滑动的距离为
当球a落到槽b中后板c的加速度
而ab的共同加速度仍为
因ab一起向右减速，而c向左减速，则当三个物体都停止运动时相对运动的位移
则木板长度L的最小值
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
