题目内容
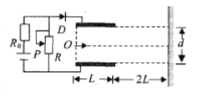
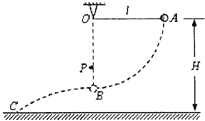
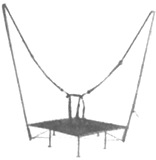
【题目】如图所示，轻质弹簧左端与墙相连，右端与质量为
的小球接触但不固连，初始时在外力作用下弹簧处于压缩状态，某时刻撤去外力，小球能顺利通过圆弧轨道ABC并无能量损失地进入圆弧轨道CDE而从E点抛出，最终打在圆弧轨道ABC的F点。已知圆弧轨道ABC的半径是圆弧轨道CDE的两倍且圆弧轨道ABC的半径
，B、D分别为圆弧轨道ABC及圆弧轨道CDE的中点。当小球离开弹簧运动到圆弧轨道A点时，对圆弧轨道的压力
，除圆弧轨道CDE外，其余部分均光滑（
）。试求：
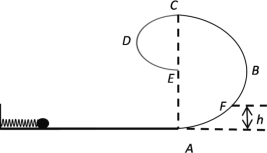
(1)小球运动到A点的速度大小及弹簧的弹性势能；
(2)小球运动到B点时，对轨道的压力大小及方向；
(3)如果F点距水平面的高度
,则小球在圆弧轨道CDE克服摩擦力所做功的取值范围为多少？
【答案】（1）
，30J（2）80N，方向向右；（3）
【解析】
（1）在A点时，由牛顿第二定律：
解得
由能量关系可知，弹簧的弹性势能为：
（2）小球运动到B点时：
，
解得
，NB=80N
则小球运动到B点时，对轨道的压力大小为80N，方向向右；
（3）若h1=0.1m，可计算得出小球从E点射出时的竖直高度H1=0.4m，水平射程：x1=0.3m，速度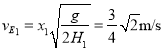
，
此时对小球由动能定理：
；
若h1=0.2m，可计算得出小球从E点射出时的竖直高度H2=0.3m，水平射程：x2=0.4m，速度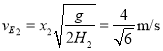
，
此时对小球由动能定理：
；
则小球在圆弧轨道CDE克服摩擦力所做功的取值范围为.
练习册系列答案
相关题目
