Question

【题目】在 “探究加速度与力、质量的关系”的实验中，

(1)如图为实验中打出的一条纸带，相邻记数点的时间间隔为0.1s，相邻两点的间距如图所示：则打下C点时小车的速度大小为_______m/s, 小车的加速度大小为________m/s2（结果保留三位有效数字）

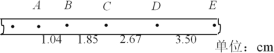
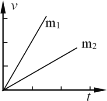
(2)不改变小车和砝码的总质量，只改变小桶中砂的质量。当砂的质量分别为m1、m2时，小车运动的v—t图象如图所示，则m1与m2相比：（_______）

A、m1=m2； B、m1>m2；　　C、m1<m2； D、无法确定。

(3)在研究加速度a与小车的质量M的关系时，由于没有注意始终满足Mm的条件，结果得到的图象应是下图中的（____）

Answer 1

【答案】0.226m/s 0.820m/s2 B D

【解析】

（1）根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上C点时小车的瞬时速度大小．

（2）小车运动的速度时间图线的斜率表示小车加速度，根据加速度大小关系求解m1、m2的关系．

（3）应用牛顿第二定律分析实验误差，然后答题．

（1）打下C点时小车的速度，
由△x=at2可知，小车的加速度，代入数据解得：a=0.820m/s2；
（2）小车运动的速度时间图线的斜率表示小车加速度，根据图1得当所挂钩码的质量为m1时小车的加速度大于所挂钩码的质量为m2时的加速度．由于不改变小车和砝码的质量，根据牛顿第二定律F=ma得当所挂钩码的质量为m1时小车的合力大于当所挂钩码的质量为m2时小车的合力，所以m1＞m2，故B正确．
（3）设绳子上拉力为F，对小车根据牛顿第二定律有：F=Ma，对砂桶和砂有：mg-F=ma，由此解得：F=，由此可知当M＞＞时，砂和砂桶的重力等于绳子的拉力，随着增大，小车质量在减小，因此小车质量不再满足远大于砂和小砂桶的质量，加速度不可能一直均匀增大，加速度的增大幅度将逐渐减小，最后趋近与定值g，故ABC错误，D正确．