题目内容
8. 如图,在匀强磁场中有一倾斜的平行光滑金属导轨,导轨间距为L=30cm,长度为d=l00cm,导轨平面与水平面的夹角为θ=37°匀强磁场的磁感应强度大小为B=2.0T,方向与导轨平面垂直.质量m=60g,电阻r=0.5Ω的导体棒从导轨的顶端由静止释放,在滑到导轨底端之前已经达到最大速度.导体棒始终与导轨垂直,接在两导轨间的电阻为R=1.5Ω,导轨电阻不计,重加速度为g=10m/s2,sin37°=0.6.求:
如图,在匀强磁场中有一倾斜的平行光滑金属导轨,导轨间距为L=30cm,长度为d=l00cm,导轨平面与水平面的夹角为θ=37°匀强磁场的磁感应强度大小为B=2.0T,方向与导轨平面垂直.质量m=60g,电阻r=0.5Ω的导体棒从导轨的顶端由静止释放,在滑到导轨底端之前已经达到最大速度.导体棒始终与导轨垂直,接在两导轨间的电阻为R=1.5Ω,导轨电阻不计,重加速度为g=10m/s2,sin37°=0.6.求:(1)电阻R上的最大功率;
(2)整个运动过程中,电阻R上产生的热量Q.
分析 (1)当导体棒受力平衡时,即重力沿斜面的分力等于安培力时,速度达最大,此时电阻上消耗的功率最大,由法拉第电磁感应定律和闭合电路欧姆定律定律求最大电流,由$P={I}_{m}^{2}R$求R上的最大功率;
(2)根据能量守恒求出回路中的总热量,因为R和r串联,所以${Q}_{R}^{\;}=\frac{R}{R+r}Q$求出R上产生的热量
解答 解:(1)导体棒沿斜面下滑时感应电动势为E,电路中的感应电流为I,安培力为F
感应电动势为:E=BLv…①
电路电流为:$I=\frac{E}{R+r}$…②
安培力为:F=BIL…③
当导体棒重力沿斜面的分力和安培力F相等时达到最大速度${v}_{m}^{\;}$,此时电阻R的功率最大,为:
安培力和重力的分力平衡,有:F=mgsinθ…④
联立①②③④得:$\frac{{B}_{\;}^{2}{L}_{\;}^{2}{v}_{m}^{\;}}{R+r}=mgsinθ$
得:${v}_{m}^{\;}=\frac{mg(R+r)sinθ}{{B}_{\;}^{2}{L}_{\;}^{2}}$
代入数据得:${v}_{m}^{\;}=2m/s$
电阻R上的最大功率:$P={I}_{\;}^{2}R=(\frac{BL{v}_{m}^{\;}}{R+r})_{\;}^{2}R=(\frac{2×0.3×2}{1.5+0.5})_{\;}^{2}×1.5=0.54W$
(2)根据能量守恒定律可知整个过程中回路产生的总电热为:
$Q=mgdsinθ-\frac{1}{2}m{v}_{m}^{2}=0.24J$
所以电阻R上产生的电热:${Q}_{R}^{\;}=\frac{R}{R+r}Q=\frac{1.5}{1.5+0.5}×0.24=0.18J$
答:(1)电阻R上的最大功率0.54W;
(2)整个运动过程中,电阻R上产生的热量Q为0.18J
点评 本题实质是力学的共点力平衡与电磁感应的综合,都要求正确分析受力情况,运用平衡条件列方程,关键要正确推导出安培力与速度的关系式,分析出能量是怎样转化的.

 53天天练系列答案
53天天练系列答案 如图所示,用静电计可以测量已充电的平行板电容器两极板之间的电势差,现使B板带电,则下列判断正确的是( )
如图所示,用静电计可以测量已充电的平行板电容器两极板之间的电势差,现使B板带电,则下列判断正确的是( )| A. | 增大两极之间的距离,指针张角变大 | |
| B. | 将金属板插入两板之间,则静电计指针张角将变大 | |
| C. | 若将玻璃板插入两板之间,则静电计指针张角变大 | |
| D. | 若将A板拿走,则静电计指针张角变为零 |
| A. | P2=2P1 | B. | P2=4P1 | C. | P2=8P1 | D. | P2=64P1 |
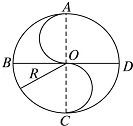 一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )
一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )| A. | 2πR $\sqrt{2}$R向西南 | B. | 4πR 2R向东南 | C. | 2.5πR $\sqrt{2}$R向东南 | D. | 3πR R向西北 |
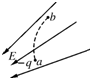 如图,实线表示某电场的电场线,一带负电的粒子沿虚线所示的路径从a点运动到b点,则( )
如图,实线表示某电场的电场线,一带负电的粒子沿虚线所示的路径从a点运动到b点,则( )| A. | 带电粒子所受电场力变大 | B. | 带电粒子所受电场力变小 | ||
| C. | 带电粒子的电势能变小 | D. | 带电粒子的电势能变大 |
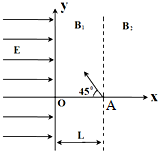 在直角坐标系的二、三象限内有沿x轴正向的匀强电场,场强大小为E,在一、四象限内以x=L的直线为理想边界的左右两侧存在垂直于纸面向里的匀强磁场B1和B2,y轴为电场与磁场的理想边界.在x轴上x=L的A点有一个质量为m、带电荷量为+q的粒子以速度v沿与x轴负方向成45°的夹角垂直于磁场射出.粒子到达y轴时速度方向与y轴刚好垂直.若带电粒子经历在电场和磁场中的一系列运动后刚好能够返回A点.不计粒子的重力
在直角坐标系的二、三象限内有沿x轴正向的匀强电场,场强大小为E,在一、四象限内以x=L的直线为理想边界的左右两侧存在垂直于纸面向里的匀强磁场B1和B2,y轴为电场与磁场的理想边界.在x轴上x=L的A点有一个质量为m、带电荷量为+q的粒子以速度v沿与x轴负方向成45°的夹角垂直于磁场射出.粒子到达y轴时速度方向与y轴刚好垂直.若带电粒子经历在电场和磁场中的一系列运动后刚好能够返回A点.不计粒子的重力