题目内容
11.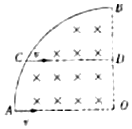 如图所示,AOB为一边界为1/4圆的匀强磁场,O点为圆心,D点为边界OB的中点,C点为边界上一点,且CD∥AO.现有两个带正电粒子1、2,它们的比荷之比为1:2,射入磁场的速率之比为1:2,其中粒子1从A点正对圆心射入,恰从B点射出,粒子2从C点沿CD射入,从某点离开磁场,不计重力及粒子间的相互作用,则( )
如图所示,AOB为一边界为1/4圆的匀强磁场,O点为圆心,D点为边界OB的中点,C点为边界上一点,且CD∥AO.现有两个带正电粒子1、2,它们的比荷之比为1:2,射入磁场的速率之比为1:2,其中粒子1从A点正对圆心射入,恰从B点射出,粒子2从C点沿CD射入,从某点离开磁场,不计重力及粒子间的相互作用,则( )| A. | 粒子2必在B、C之间(不含B、C)某点射出磁场 | |
| B. | 粒子2必在D、B之间(不含D、B)某点射出磁场 | |
| C. | 粒子1与粒子2在磁场中的运行时间之比为3:2 | |
| D. | 粒子1与粒子2的速度偏转角度之比为3:2 |
分析 粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律求出粒子的轨道半径,作出粒子的运动轨迹,应用数学知识与牛顿第二定律分析答题.
解答 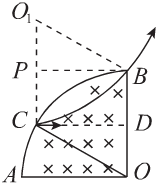 解:粒子在磁场中做匀速圆周运动洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,解得:r=$\frac{mv}{qB}$,
解:粒子在磁场中做匀速圆周运动洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,解得:r=$\frac{mv}{qB}$,
由题意可知,两粒子的比荷之比为1:2,射入磁场的速率之比为1:2,则它们的轨道半径相等,即:r1=r2,
A、粒子运动轨迹如图所示,粒子1从A点正对圆心射入,恰从B点射出,粒子在你磁场中运动的圆心角为90°,粒子轨道半径等于BO,
粒子2从C点沿CD射入其运动轨迹如图所示,设对应的圆心为O1,运动轨道半径也为:BO=R,连接O1C、O1B,
O1COB是平行四边形,O1B=CO,则粒子2一定从B点射出磁场,故AB错误;
C、粒子1的速度偏角,粒子在磁场中转过的圆心角θ1=90°,连接PB,可知P为O1C的中点,由数学知识可知,θ2=∠BO1P=60°,两粒子的速度偏角不同,粒子在磁场中运动的周期:T=$\frac{2πm}{qB}$,由于两粒子的比荷之比为1:2,则:$\frac{{T}_{1}}{{T}_{2}}$=$\frac{2}{1}$,粒子在磁场中的运动时间:
t=$\frac{θ}{2π}$T,它们在磁场中的运动时间之比:$\frac{{t}_{1}}{{t}_{2}}$=$\frac{{θ}_{1}{T}_{1}}{{θ}_{2}{T}_{2}}$=$\frac{90°}{60°}$×$\frac{2}{1}$=$\frac{3}{1}$,粒子1与粒子2的速度偏转角度之比:θ1:θ2=90°:60°=3:2,故C错误,D正确;
故选:D.
点评 本题考查了粒子在匀强磁场中的运动,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,作出粒子运动轨迹、应用数学知识、周期公式即可正确解题.

 名校课堂系列答案
名校课堂系列答案| A. | 速度变化大小为g△t,方向竖直向下 | |
| B. | 动量变化量大小为△P=m(v2-v1),方向竖直向下 | |
| C. | 动量变化量大小为△P=mg△t,方向竖直向下 | |
| D. | 动能变化为△Ek=$\frac{1}{2}$m(v22-v12) |
| A. |  | B. |  | C. |  | D. |  |
| A. | 若一个力对物体不做功,说明该物体一定没有位移 | |
| B. | 人用力F=300N将足球踢出,球在空中飞行40m,人对足球做功12000J | |
| C. | 由P=$\frac{W}{t}$ 可知,力做的功越多,功率越大 | |
| D. | 由P=Fvcosα可知,某一时刻,即使力和速度都很大,但功率不一定大 |
| A. | 弹簧越长,弹性势能越大 | |
| B. | 弹簧处于原长时,弹性势能为0 | |
| C. | 弹簧的压缩量和伸长量相等时,弹性势能相等 | |
| D. | 用一水平力缓慢拉一水平固定的弹簧,外力做功越多,弹性势能越小 |
 2016年里约奥运会女子10米跳台,小将任茜获得金牌.她从跳台斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力.下列说法正确的是( )
2016年里约奥运会女子10米跳台,小将任茜获得金牌.她从跳台斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力.下列说法正确的是( )| A. | 她在空中上升过程中处于超重状态 | |
| B. | 她在空中下落过程中处于失重状态 | |
| C. | 她即将入水时的速度为整个跳水过程中的最大速度 | |
| D. | 入水过程中,她对水的作用力大小大于水对她的作用力 |