题目内容
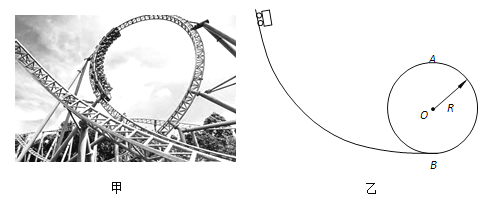
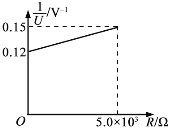
【题目】如图所示,质量为m的小物块放在长直水平面上,用水平细线紧绕在半径为R、质量为2m的薄壁圆筒上.t=0时刻,圆筒在电动机带动下由静止开始绕竖直中心轴转动,转动中角速度满足ω=β1t(β1为已知常数),物块和地面之间动摩擦因数为μ,则从开始运动至t=t1时刻,电动机做了多少功?

【答案】μmg![]() +
+ ![]()
【解析】试题分析:物体运动速度与线速度相同,则由圆的转动情况可知物体的运动情况,根据圆的线速度的变化可以求得加速度的大小,再由牛顿第二定律可求得合外力;由动能定理可求得拉力所做的功。
圆筒边缘线速度与物块前进速度大小相同,根据v=ωR=Rβ1t,线速度与时间成正比
物块做初速为零的匀加速直线运动且加速度为a= Rβ1
根据物块受力,由牛顿第二定律得 T-μmg=ma
则细线拉力为 T=μmg+m Rβ1
对整体运用能量关系,有
![]()
其中![]()
则电动机做的功为 :![]()

练习册系列答案
相关题目