题目内容
如下图所示,一个质量为M的人,站在台秤上,一长为R的悬线一端系一个质量为m小球,手拿悬线另一端,小球绕悬线另一端点在竖直平面内做圆周运动,且小球恰好能通过圆轨道最高点,则下列说法正确是( ) 
| A.小球运动到最低点时,台秤的示数最大且为(M+6m)g |
| B.小球运动到最高点时,台秤的示数最小且为Mg |
| C.小球在a、b、c三个位置台秤的示数相同 |
| D.小球从最高点运动到最低点的过程中台秤的示数增大,人处于超重状态 |
AC
解析试题分析:小球运动到最低点时,加速度竖直向上,根据牛顿第二定律,运用整体法,台秤的支持力应该大于总重力才行,且此时最大,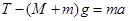 ,而向心力
,而向心力 ,在竖直面内机械能守恒,则有
,在竖直面内机械能守恒,则有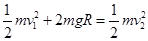 ,而小球恰能经过最高点,有
,而小球恰能经过最高点,有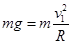 ,联系以上各式得选项A正确。在a、b、c三个位置,小球在竖直方向的加速度都是重力加速度,因此根据刚才的分析,台秤的支持力相等,选项C正确、B错误。人始终静止不动,处于平衡状态,选项D错误。
,联系以上各式得选项A正确。在a、b、c三个位置,小球在竖直方向的加速度都是重力加速度,因此根据刚才的分析,台秤的支持力相等,选项C正确、B错误。人始终静止不动,处于平衡状态,选项D错误。
考点:本题考查牛顿第二定律,涉及超重和失重,向心力以及整体法和隔离法。

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案如图所示,在光滑平面上有一静止小车,小车上静止地放置着一小物块,物块和小车间的动摩擦因数为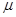 =0.3,用水平恒力F拉动小车,下列关于物块的加速度
=0.3,用水平恒力F拉动小车,下列关于物块的加速度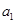 和小车的加速度
和小车的加速度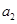 。当水平恒力F取不同值时,
。当水平恒力F取不同值时,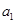 与
与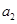 的值可能为(当地重力加速度g取
的值可能为(当地重力加速度g取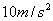 )( )
)( )
A.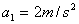 , ,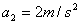 |
B.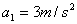 , ,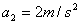 |
C. , ,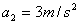 |
D.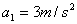 , ,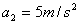 |
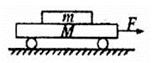
如图所示,在光滑平面上有一静止小车,小车质量为M=5kg,小车上静止地放置着质量为m=1kg的木块,和小车间的动摩擦因数为μ=0.2,用水平恒力F拉动小车,下列关于木块的加速度am和小车的加速度aM,可能正确的有( )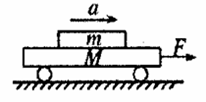
| A.am=1 m/s2, aM=1 m/s2 |
| B.am=1 m/s2, aM=2 m/s2 |
| C.am=2 m/s2, aM=4 m/s2 |
| D.am=3 m/s2, aM=5 m/s2 |
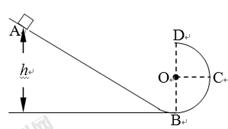
在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率 =
= , 则下述正确的是 ( )
, 则下述正确的是 ( )
A.此小球的最大速率是  |
B.小球到达C点时对轨道的压力是 |
C.小球沿圆轨道绕行一周所用的时间小于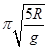 |
| D.小球在任一直径两端点上的动能之和相等 |
某位同学为了研究超重和失重现象,将重为50N的物体带到电梯中,并将它放在水平放置的传感器上,电梯由启动到停止的过程中,测得重物的压力随时间变化的图象如图所示。设在t1=2s和t2=8s时电梯的速度分别为v1和v2。下列判断正确的是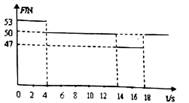
| A.电梯在上升,v1>v2 |
| B.电梯在上升,v2>v1 |
| C.电梯在下降,v1>v2 |
| D.电梯在下降,v2>v1 |
放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间t的关系如图所示。取重力加速度g="10" m/s2。由此两图线可以求得物块的质量m和物块与地面之间的动摩擦因数μ分别为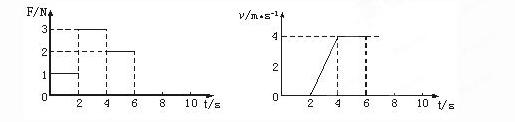
| A.m="0.5" kg,μ=0.4 |
| B.m="1.5" kg,μ=2/15 |
| C.m="0.5" kg,μ=0.2 |
| D.m="1" kg,μ=0.2 |
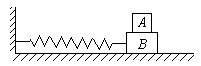
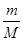 )kx D.(
)kx D.(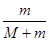 )kx
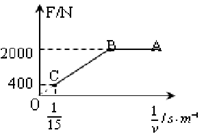
)kx kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出 图象(图中AB、BO均为直线),假设电动车行驶过程中所受的阻力恒定,则
kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出 图象(图中AB、BO均为直线),假设电动车行驶过程中所受的阻力恒定,则