题目内容
在竖直平面内有一半径为R的光滑圆环轨道，一质量为m的小球穿在圆环轨道上做圆周运动，到达最高点C时的速率
=
, 则下述正确的是 （ ）
A．此小球的最大速率是  |
B．小球到达C点时对轨道的压力是 |
C．小球沿圆轨道绕行一周所用的时间小于 |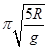
| D．小球在任一直径两端点上的动能之和相等 |
ACD
解析试题分析：速度最大的点应该是最低点时，根据动能定理：
,解得: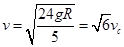
所以A正确．在C点有：
，得
，所以B错误；由
，当速度最小时，代入计算可得
，之后小球的速度在变大，所以T要减小，所以
，所以C正确．整个过程中机械能守恒，在任一直径两端点上的点，它们的高度之和都是2R，即它们的重力势能的和相等，由于总的机械能守恒，所以它们的动能之和也相等，所以D正确．
考点：机械能守恒定律，牛顿第二定律，向心力．
质量为m的带正电小球由空中A点无初速度自由下落，在t秒末加上竖直向上、范围足够大的匀强电场，再经过t秒小球又回到A点。不计空气阻力且小球从未落地，则( )
| A．整个过程中小球电势能减少了1.5 mg2t2 |
| B．整个过程中机械能的增量为2 mg2t2 |
| C．从加电场开始到小球运动到最低点时小球动能减少了mg2t2 |
| D．从A点到最低点小球重力势能减少了2/3mg2t2 |
和
，以最低点Ｃ所在的水平面为重力势能参考平面，则
如图所示，一足够长的光滑斜面，倾角为
，一弹簧上端固定在斜面的顶端，下端与物体
相连，物体b上表面粗糙，在其上面放一物体a，a、b间的动摩擦因数为
(
)，将物体a、b从O点由静止开始释放，释放时弹簧恰好处于自由伸长状态，当b滑到A点时，a刚好从b上开始滑动；滑到B点时a刚好从b上滑下，b也恰好速度为零，设a、b间的最大静摩擦力等于滑动摩擦力。下列对物体a、b运动情况描述正确的是( )
A．从O到A的过程，两者一直加速，加速度大小从 一直减小，在A点减为零 |
B．经过A点时，a、b均已进入到减速状态，此时加速度大小是 |
| C．从A到B的过程中，a的加速度不变，b的加速度在增大，速度在减小 |
| D．经过B点，a掉下后，b开始反向运动但不会滑到开始下滑的O点 |
如图所示，水平木板上有质量m="1.0" kg的物块，受到随时间t变化的水平拉力F作用，用力传感器测出相应时刻物块所受摩擦力Ff的大小。取重力加速度g="10" m/s2，下列判断正确的是（ ）
| A．5 s内拉力对物块做功为零 |
| B．4 s末物块所受合力大小为4.0 N |
| C．物块与木板之间的动摩擦因数为0.4 |
| D．6 s-9 s内物块的加速度大小为2.0m/s2 |
如下图所示，一个质量为M的人，站在台秤上，一长为R的悬线一端系一个质量为m小球，手拿悬线另一端，小球绕悬线另一端点在竖直平面内做圆周运动，且小球恰好能通过圆轨道最高点，则下列说法正确是（ ） 
| A．小球运动到最低点时，台秤的示数最大且为（M＋6m）g |
| B．小球运动到最高点时，台秤的示数最小且为Mg |
| C．小球在a、b、c三个位置台秤的示数相同 |
| D．小球从最高点运动到最低点的过程中台秤的示数增大，人处于超重状态 |
一质点开始时做匀速直线运动，从某时刻起受到一恒力作用．此后，该质点的速度可能是
| A．一直不变 |
| B．先逐渐减小至零，再逐渐增大 |
| C．先逐渐减小至某一非零的最小值，再逐渐增大 |
| D．先逐渐增大至某一最大值，再逐渐减小 |
一辆运送沙子的自卸卡车装满沙子，沙粒之间的动摩擦因数为μ1，沙子与车厢底部材料的动摩擦因数为μ2，车厢的倾角用θ表示(已知μ2>μ1)，下列说法正确的是( )
| A．要顺利地卸干净全部沙子，应满足tanθ＞μ2 |
| B．要顺利地卸干净全部沙子，应满足sinθ＞μ2 |
| C．只卸去部分沙子，车上还留有一部分沙子，应满足μ2＞tanθ＞μ1 |
| D．只卸去部分沙子，车上还留有一部分沙子，应满足μ2>μ1>tanθ |
质量为m的汽车，启动后发动机以额定功率P沿水平道路行驶，经过一段时间后以速度v匀速行驶，若行驶中汽车受到的阻力大小不变，则在加速过程中车速为v/3时，汽车的加速度大小为
| A．3P/mv | B．2P/mv | C．P/mv | D．0 |