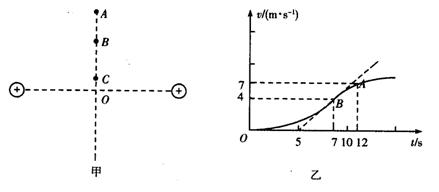
题目内容
放在水平地面上的一物块，受到方向不变的水平推力F的作用，F的大小与时间t的关系和物块速度v与时间t的关系如图所示。取重力加速度g="10" m/s2。由此两图线可以求得物块的质量m和物块与地面之间的动摩擦因数μ分别为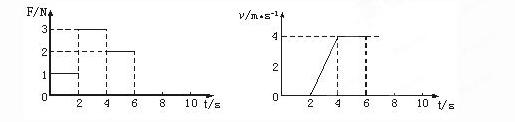
| A．m="0.5" kg，μ=0.4 |
| B．m="1.5" kg，μ=2/15 |
| C．m="0.5" kg，μ=0.2 |
| D．m="1" kg，μ=0.2 |
A
解析试题分析：根据速度图像和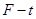
图像可知，在2～4s内物体的加速度为2m/s2，外力为3N；在4～6s内，物体匀速运动，受力平衡，故摩擦力
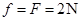，而滑动摩擦力大小不变，所以在2～4s内，由牛顿第二定律得
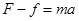，代入数据解得物体的质量
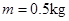；根据
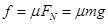，代入数据解得
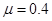，所以只有A选项正确。
考点：牛顿第二定律
世纪百通期末金卷系列答案 两孩子在社区健身器材上玩耍，不考虑绳与滑轮的质量，不计轴承摩擦、绳与滑轮间的摩擦。初始时两人均站在水平地面上；当位于左侧的甲用力向上攀爬时，位于右侧的乙始终用力抓住绳子，最终至少一人能到达滑轮。下列说法正确的是
| A．若甲的质量较大，则乙先到达滑轮 |
| B．若甲的质量较大，则甲、乙同时到达滑轮 |
| C．若甲、乙质量相同，则乙先到达滑轮 |
| D．若甲、乙质量相同，则甲先到达滑轮 |
如下图所示，一个质量为M的人，站在台秤上，一长为R的悬线一端系一个质量为m小球，手拿悬线另一端，小球绕悬线另一端点在竖直平面内做圆周运动，且小球恰好能通过圆轨道最高点，则下列说法正确是（ ） 
| A．小球运动到最低点时，台秤的示数最大且为（M＋6m）g |
| B．小球运动到最高点时，台秤的示数最小且为Mg |
| C．小球在a、b、c三个位置台秤的示数相同 |
| D．小球从最高点运动到最低点的过程中台秤的示数增大，人处于超重状态 |
利用传感器和计算机可以测量快速变化的力的瞬时值。实验时，把小球举高到弹性绳子的悬点O 处，然后放手让小球自由下落。图是用这种方法获得的弹性绳中拉力随时间的变化图线。由图所提供的信息，以下正确的是( )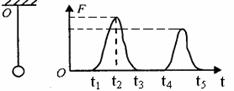 
| A．t2时刻小球速度最大 |
| B．小球和弹性绳组成的系统机械能不守恒 |
| C．t1到t2期间小球速度一直减小到零 |
| D．t1到t2期间小球重力势能减少量小于弹性绳弹性势能增加量 |
一辆运送沙子的自卸卡车装满沙子，沙粒之间的动摩擦因数为μ1，沙子与车厢底部材料的动摩擦因数为μ2，车厢的倾角用θ表示(已知μ2>μ1)，下列说法正确的是( )
| A．要顺利地卸干净全部沙子，应满足tanθ＞μ2 |
| B．要顺利地卸干净全部沙子，应满足sinθ＞μ2 |
| C．只卸去部分沙子，车上还留有一部分沙子，应满足μ2＞tanθ＞μ1 |
| D．只卸去部分沙子，车上还留有一部分沙子，应满足μ2>μ1>tanθ |
如图5所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力．已知AP＝2R，重力加速度为g，则小球从P到B的运动过程中 
| A．重力做功2mgR | B．机械能减少mgR | C．合外力做功mgR | D．克服摩擦力做功 mgR |
某科技创新小组设计制作出一种全自动升降机模型，用电动机通过钢丝绳拉着升降机由静止开始匀加速上升，已知升降机的质量为m，当升降机的速度为v1时，电动机的有用功率达到最大值P，以后电动机保持该功率不变，直到升降机以最大速度v2匀速上升为止，整个过程中忽略摩擦阻力及空气阻力，重力加速度为g。有关此过程下列说法正确的是（ ）
| A．钢丝绳的最大拉力为P/v2 |
| B．升降机的最大速度v2=p/mg |
| C．钢丝绳的拉力对升降机所做的功等于升降机克服重力所做的功 |
| D．升降机速度由v1增大至v2的过程中，钢丝绳的拉力不断减小 |
如图所示，绝缘弹簧的下端固定在光滑斜面底端，弹簧与斜面平行，带电小球Q（可视为质点）固定在绝缘斜面上的M点，且在通过弹簧中心的直线ab上．现将与Q大小相同，带电性也相同的小球P，从直线ab上的N点由静止释放，若两小球可视为点电荷．在小球P与弹簧接触到速度变为零的过程中，下列说法中正确的是（ ）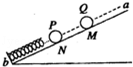
| A．小球P的速度一定先增大后减小 |
| B．小球P的机械能一定在减少 |
| C．小球P速度最大时所受弹簧弹力和库仑力的合力为零 |
| D．小球P与弹簧系统的机械能一定增加 |