题目内容
20.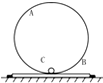 如图,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放一小球C,A,B,C的质量均为m,给线圈一水平向右的瞬时速度v,小球会在环内做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,(不计小球与环的摩擦力),最大瞬时速度v为( )
如图,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放一小球C,A,B,C的质量均为m,给线圈一水平向右的瞬时速度v,小球会在环内做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,(不计小球与环的摩擦力),最大瞬时速度v为( )| A. | $\sqrt{4gr}$ | B. | $\sqrt{6gr}$ | C. | $\sqrt{5gr}$ | D. | $\sqrt{7gr}$ |
分析 小球在环内侧做圆周运动,通过最高点速度最小时,轨道对球的最小弹力为零;为了不会使环在竖直方向上跳起,小球在最高点对轨道的弹力不能大于2mg,根据牛顿第二定律求出最高点的最大速度,再根据机械能守恒定律求出小球在最低点的速度范围.
解答 解:在最高点,要不会使环在竖直方向上跳起,环对球的压力最大为:
F=2mg
则环在最高点:$3mg=\frac{m{v}_{1}^{2}}{r}$
从最高点到最低点的过程中,机械能守恒,设此时最低点的速度为v2,
解得:v1=$\sqrt{3gr}$.
根据机械能守恒定律有:2mgR+$\frac{1}{2}$mv12=$\frac{1}{2}$mv22
解得:v2=$\sqrt{7gr}$.故D正确,ABC错误.
故选:D.
点评 本题综合考查了牛顿第二定律和机械能守恒定律,关键理清在最高点的两个临界情况,求出在最高点的最大速度.

练习册系列答案
相关题目
10.关于电容器、电感器在电路中的作用,下列说法正确的是( )
| A. | 隔直电容器在电路中,通交流阻直流 | |
| B. | 旁路电容器在电路中,通低频阻高频 | |
| C. | 低频扼流圈在电路中,通交流阻直流 | |
| D. | 高频扼流圈在电路中,通高频阻低频 |
15.以速度v0水平抛出一球,某时刻其竖直分位移与水平位移相等,以下判断正确的是( )
| A. | 竖直分速度等于水平分速度 | B. | 此时球的速度大小为$\sqrt{5}$v0 | ||
| C. | 运动的时间为$\frac{\sqrt{5}}{g}$v0 | D. | 运动的位移是$\frac{2\sqrt{2}}{g}$v0 |
10. 如图所示,质量相等的A、B两物体紧贴在匀速转动的圆筒的竖直内壁上随圆筒一起做匀速圆周运动,则下列关系正确的有( )
如图所示,质量相等的A、B两物体紧贴在匀速转动的圆筒的竖直内壁上随圆筒一起做匀速圆周运动,则下列关系正确的有( )
 如图所示,质量相等的A、B两物体紧贴在匀速转动的圆筒的竖直内壁上随圆筒一起做匀速圆周运动,则下列关系正确的有( )
如图所示,质量相等的A、B两物体紧贴在匀速转动的圆筒的竖直内壁上随圆筒一起做匀速圆周运动,则下列关系正确的有( )| A. | 线速度vA=vB | B. | 它们受到的摩擦力fA>fB | ||
| C. | 运动周期TA>TB | D. | 筒壁对它们的弹力NA>NB |

 如图所示,将多用表的选择开关置于“欧姆档”,再将电表的两支表笔与负温度系数的热敏电阻Rt的两端相连,这时表针恰好指在刻度的正中间.若往Rt上擦一些酒精,表针将向左(填“左”或“右”)偏;若用吹风机将热风吹向电阻,表针将向右(填“左”或“右”)偏.
如图所示,将多用表的选择开关置于“欧姆档”,再将电表的两支表笔与负温度系数的热敏电阻Rt的两端相连,这时表针恰好指在刻度的正中间.若往Rt上擦一些酒精,表针将向左(填“左”或“右”)偏;若用吹风机将热风吹向电阻,表针将向右(填“左”或“右”)偏. A、B小球在一条竖直线上,相聚H=10m,A、B、C三个小球同时以相同速率向不同的方向抛出,A竖直向下抛,B竖直向上抛,C想A、B所在的竖直线平抛,经0.5s三个球在空中相遇,g=10m/s2.求:
A、B小球在一条竖直线上,相聚H=10m,A、B、C三个小球同时以相同速率向不同的方向抛出,A竖直向下抛,B竖直向上抛,C想A、B所在的竖直线平抛,经0.5s三个球在空中相遇,g=10m/s2.求: 如图所示是弹簧振子的振动图象,从图象中可以看出:振子的振幅是10cm、频率是25 Hz.振子在4s内通过的路程是40m,该简谐运动的表达式为y=10sin50πt(cm).
如图所示是弹簧振子的振动图象,从图象中可以看出:振子的振幅是10cm、频率是25 Hz.振子在4s内通过的路程是40m,该简谐运动的表达式为y=10sin50πt(cm).