题目内容
3.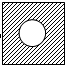 有一根细长而均匀的金属材料,长为l,电阻率为ρ,横戴面积外方(正方形)内圆,正方形边长为a,如图所示,现把它沿垂直纸面方向接入电路中,当电压为U时,电流为I,内圆的直径为多大?
有一根细长而均匀的金属材料,长为l,电阻率为ρ,横戴面积外方(正方形)内圆,正方形边长为a,如图所示,现把它沿垂直纸面方向接入电路中,当电压为U时,电流为I,内圆的直径为多大?
分析 由R=$\frac{U}{I}$可求得其阻值,再由R=$ρ\frac{L}{S}$可确定其S,再求得其直径.
解答 解:设直径为d,则有:$\frac{U}{I}$=$ρ\frac{l}{{a}^{2}-π(\frac{d}{2})2}$
可得:d=$\sqrt{\frac{4Iρl}{πU}-\frac{4{a}^{2}}{π}}$
答:内圆的直径为$\sqrt{\frac{4Iρl}{πU}-\frac{4{a}^{2}}{π}}$
点评 明确R=$\frac{U}{I}$再结合R=$ρ\frac{L}{S}$求解,基本内容,不难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.在做“验证力的平行四边形定则”实验时,橡皮条的一端固定在木板上,一次用两个弹簧秤分别拉着两根绳套把橡皮条的另一端拉到某一确定的O点,另一次是用一个弹簧秤通过细绳把橡皮条的另一端拉到O点,则下列说法中正确的是( )
| A. | 同一次实验中,O点位置不允许变动 | |
| B. | 实验中,橡皮条、细绳和弹簧秤应与木板保持平行 | |
| C. | 实验中,把橡皮条的另一端拉到O点时,两个弹簧秤之间的夹角必须取90° | |
| D. | 拉橡皮条的细绳要适当长些,标记同一细绳方向的两点要稍远些 |
18.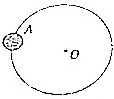 如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆,已知引力常量为G,天文学家测得到A行星的运行轨道半径为R0,周期为T0.天文学家经过长期观测发现,A行星其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则下列说法正确的是( )
如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆,已知引力常量为G,天文学家测得到A行星的运行轨道半径为R0,周期为T0.天文学家经过长期观测发现,A行星其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则下列说法正确的是( )
 如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆,已知引力常量为G,天文学家测得到A行星的运行轨道半径为R0,周期为T0.天文学家经过长期观测发现,A行星其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则下列说法正确的是( )
如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆,已知引力常量为G,天文学家测得到A行星的运行轨道半径为R0,周期为T0.天文学家经过长期观测发现,A行星其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则下列说法正确的是( )| A. | 行星A的向心加速度大于中央恒星O表面的重力加速度 | |
| B. | 行星A运行的线速度小于中央恒星O的第一宇宙速度 | |
| C. | 中央恒星O的质量为$\frac{4{π}^{2}{{R}^{3}}_{0}}{G{{T}^{2}}_{0}}$ | |
| D. | 行星B运行的周期T=t0+T0 |
8.下雨天,假设无风,雨滴以速度υ1竖直下落,雨滴在空中的分布是均匀的,单位体积的雨量是ρ,一个人要从A处匀速运动到B处,他没有带伞,A、B的距离为l,人的运动速度为υ2.在计算打到身上的雨量时,把人简化为长方体模型,头和肩的水平面积为S1,身体前方正面的竖直面积为S2.则( )
| A. | 从A到B的过程中,打到面积S1上的雨量为ρS1v1$\frac{l}{{v}_{2}}$ | |
| B. | 从A到B的过程中,打到人身上上的雨量为ρS1v1$\frac{l}{{v}_{2}}$+ρS2l | |
| C. | 把人简化为长方体模型是不切实际的 | |
| D. | 从A到B的过程中,无法判断打到人身上的雨量 |

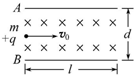 如图所示,A、B为一对平行板,板长为L,两板距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,一个质量为m,带电荷量为+q的带电粒子以初速度v0,从A、B两板左边缘的中间沿垂直于磁感线的方向射入磁场.求v0在什么范围内,粒子才能从磁场内射出?
如图所示,A、B为一对平行板,板长为L,两板距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,一个质量为m,带电荷量为+q的带电粒子以初速度v0,从A、B两板左边缘的中间沿垂直于磁感线的方向射入磁场.求v0在什么范围内,粒子才能从磁场内射出?
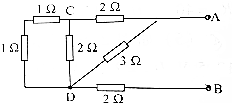 写出如图所示的任意两点间等效电阻值.
写出如图所示的任意两点间等效电阻值.