题目内容
18.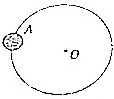 如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆,已知引力常量为G,天文学家测得到A行星的运行轨道半径为R0,周期为T0.天文学家经过长期观测发现,A行星其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则下列说法正确的是( )
如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆,已知引力常量为G,天文学家测得到A行星的运行轨道半径为R0,周期为T0.天文学家经过长期观测发现,A行星其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则下列说法正确的是( )| A. | 行星A的向心加速度大于中央恒星O表面的重力加速度 | |
| B. | 行星A运行的线速度小于中央恒星O的第一宇宙速度 | |
| C. | 中央恒星O的质量为$\frac{4{π}^{2}{{R}^{3}}_{0}}{G{{T}^{2}}_{0}}$ | |
| D. | 行星B运行的周期T=t0+T0 |
分析 由万有引力提供向心力可求得速度与半径r的关系,并可求得中心天体的质量;先根据多转动一圈时间为t0,求出卫星的周期;
解答 解:A、由a=$\frac{GM}{{r}^{2}}$,可知半径大的加速度小,则A错误
B、$;v=\sqrt{\frac{GM}{r}}$可知行星A运行的线速度小于中央恒星O的第一宇宙速度,则B正确
C、由$;\\;mr\frac{4{π}^{2}}{{T}_{0}^{2}}$$mr\frac{4{π}^{2}}{{T}_{0}^{2}}$=G$\frac{Mm}{{r}^{2}}$可得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}_{0}^{2}}$=$\frac{4{π}^{2}{{R}^{3}}_{0}}{G{{T}^{2}}_{0}}$,则C正确
D、由题意可知:A、B相距最近时,B对A的影响最大,且每隔时间t0发生一次最大的偏离,说明A、B相距最近,设B行星的周期为T,则有:$(\frac{2π}{{T}_{0}}-\frac{2π}{T}){t}_{0}=2π$ 解得:T=$\frac{{t}_{0}{T}_{0}}{{t}_{0}-{T}_{0}}$则D错误
故选:BC
点评 要注意已知旋转天体的轨道半径和周期求出的是中心天体的质量,而不是旋转天体本身的质量,掌握万有引力提供向心力这一理论,并能灵活运用,知道A、B相距最近时,B对A的影响最大,且每隔时间t0发生一次最大的偏离,说明A、B相距最近,难度适中.

练习册系列答案
相关题目
8.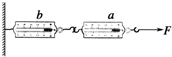 如图所示,将两弹簧测力计a、b连结在一起,当用力缓慢拉a弹簧测力计时,发现不管拉力F多大(未超出量程),a、b两弹簧测力计的示数总是相等,这个实验说明( )
如图所示,将两弹簧测力计a、b连结在一起,当用力缓慢拉a弹簧测力计时,发现不管拉力F多大(未超出量程),a、b两弹簧测力计的示数总是相等,这个实验说明( )
 如图所示,将两弹簧测力计a、b连结在一起,当用力缓慢拉a弹簧测力计时,发现不管拉力F多大(未超出量程),a、b两弹簧测力计的示数总是相等,这个实验说明( )
如图所示,将两弹簧测力计a、b连结在一起,当用力缓慢拉a弹簧测力计时,发现不管拉力F多大(未超出量程),a、b两弹簧测力计的示数总是相等,这个实验说明( )| A. | 这是两只完全相同的弹簧测力计 | |
| B. | 弹力的大小与弹簧的形变量成正比 | |
| C. | 两弹簧测力计彼此之间受到的力是一对平衡力 | |
| D. | 作用力与反作用力大小相等、方向相反 |
9.我国已经成功发射北斗COMPASS-G1地球同步卫星.据了解这已是北斗卫星导航系统发射的第三颗地球同步卫星.则对于这三颗已发射的同步卫星,下列说法中正确的是( )
| A. | 它们的运行速度大小相等,且都大于7.9 km/s | |
| B. | 它们的运行周期可能不同 | |
| C. | 它们离地心的距离可能不同 | |
| D. | 它们的角速度与静止在赤道上物体的角速度相同 |
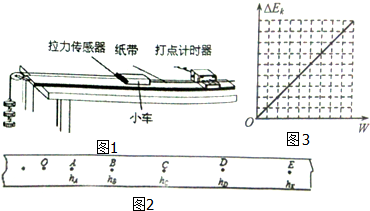
18.如图2为“探究做功和物体速度变化关系”的实验装置,小车在并在一起的相同的伸长橡皮筋作用下弹出,沿木板滑行,获得的速度由打点计时器所打的纸带测出.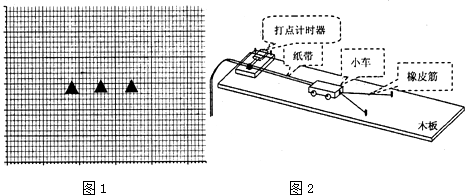
(1)实验中通过改变橡皮筋的数量,而不是改变橡皮筋的伸长量,来探究橡皮筋对小车的做功情况,这样做的好处是便于定量表示橡皮筋做功的大小.
(2)为了保证合力对小车所做的功就等于橡皮筋所做的功,实验可采用垫高斜面末端,平衡摩擦力的措施.(3)下表为一同学实验记录的数据,W代表一根橡皮筋所做的功.请运用表中测定的数 据如图1所示的坐标系中作出相应的图象,进一步可探究出橡皮筋做的功Wn和物体速度vn变化的关系为:Wn与vn2成正比.

| 橡皮筋做功Wn | 10个间隔距离x(m) | 10个间隔时间T(s) | 小车获得速度vn(m/s) | 小车速度的平方vn(m/s)${\;}^{{2}^{2}}$ | |
| 1 | W | 0.2880 | 0.2 | 1.44 | 2.07 |
| 2 | 2W | 0.4176 | 0.2 | 2.09 | 4.36 |
| 3 | 3W | 0.4896 | 0.2 | 2.45 | 5.99 |
| 4 | 4W | 0.5904 | 0.2 | 2.95 | 8.71 |
| 5 | 5W | 0.6480 | 0.2 | 3.24 | 10.50 |
(2)为了保证合力对小车所做的功就等于橡皮筋所做的功,实验可采用垫高斜面末端,平衡摩擦力的措施.(3)下表为一同学实验记录的数据,W代表一根橡皮筋所做的功.请运用表中测定的数 据如图1所示的坐标系中作出相应的图象,进一步可探究出橡皮筋做的功Wn和物体速度vn变化的关系为:Wn与vn2成正比.
19.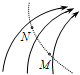 某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
 某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )| A. | 粒子带负电 | |
| B. | 粒子在M点的加速度大 | |
| C. | 粒子在N点的速度小 | |
| D. | 粒子在M点的电势能比在N点的电势能大 |
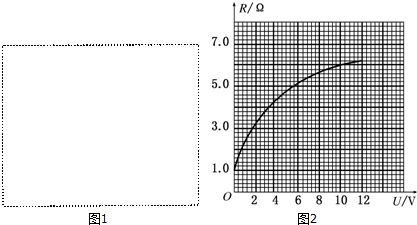
 如图所示,有一小磁针静止在条形磁铁的上方,试标出小磁针的极性.
如图所示,有一小磁针静止在条形磁铁的上方,试标出小磁针的极性.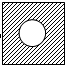 有一根细长而均匀的金属材料,长为l,电阻率为ρ,横戴面积外方(正方形)内圆,正方形边长为a,如图所示,现把它沿垂直纸面方向接入电路中,当电压为U时,电流为I,内圆的直径为多大?
有一根细长而均匀的金属材料,长为l,电阻率为ρ,横戴面积外方(正方形)内圆,正方形边长为a,如图所示,现把它沿垂直纸面方向接入电路中,当电压为U时,电流为I,内圆的直径为多大?