题目内容
11.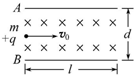 如图所示,A、B为一对平行板,板长为L,两板距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,一个质量为m,带电荷量为+q的带电粒子以初速度v0,从A、B两板左边缘的中间沿垂直于磁感线的方向射入磁场.求v0在什么范围内,粒子才能从磁场内射出?
如图所示,A、B为一对平行板,板长为L,两板距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,一个质量为m,带电荷量为+q的带电粒子以初速度v0,从A、B两板左边缘的中间沿垂直于磁感线的方向射入磁场.求v0在什么范围内,粒子才能从磁场内射出?
分析 粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,作出粒子运动轨迹,求出粒子恰好射出磁场的临界半径,应用牛顿第二定律求出粒子的临界速度,然后确定粒子的速度范围.
解答 解:粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qv0B=m$\frac{{v}_{0}^{2}}{r}$,
解得:v0=$\frac{qBr}{m}$,
粒子恰好从磁场射出的运动轨迹如图所示: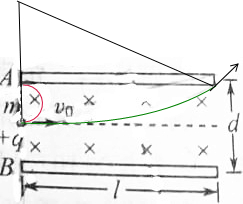
由几何知识可知,粒子恰好从磁场左边射出时,
轨道半径:r1=$\frac{d}{4}$,粒子要从左边界射出磁场,
轨道半径:r≤r1=$\frac{d}{4}$,粒子的速度:v0≤$\frac{qBd}{4m}$,
粒子恰好从磁场右边界射出此时时,轨道半径为r2,
由几何知识可知:(r2-$\frac{d}{2}$)2+L2=r22,
解得:r2=$\frac{d}{4}$+$\frac{{L}^{2}}{d}$,
粒子从磁场右边界射出时,r≥r2=$\frac{d}{4}$+$\frac{{L}^{2}}{d}$,
速度为:v0≥$\frac{qB({d}^{2}+4{L}^{2})}{4md}$;
答:粒子能从磁场内射出的速度v0的范围是v0≤$\frac{qBd}{4m}$或v0≥$\frac{qB({d}^{2}+4{L}^{2})}{4md}$.
点评 本题考查了粒子在磁场中的运动,考查了求粒子的速度范围,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键,应用牛顿第二定律可以解题,解题时注意几何知识的应用.

练习册系列答案
相关题目
2.物体做自由落体运动的过程中,下列说法正确的是( )
| A. | 物体的加速度越来越大 | B. | 物体所受重力的瞬时功率越来越大 | ||
| C. | 物体的重力势能越来越小 | D. | 物体的动能越来越小 |
19.如图所示,弹簧测力计和细线的重力及一切摩擦不计,重物的重力G=3N,则弹簧测力计A和B的示数分别为( )


| A. | 3N,0 | B. | 3N,3N | C. | 1.5N,1.5N | D. | 0,3N |
11.三个阻值都为18Ω的电阻,它们任意连接、组合,总电阻不可能为( )
| A. | 6Ω | B. | 27Ω | C. | 8Ω | D. | 54Ω |
12.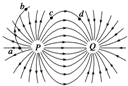 P、Q两电荷的电场线分布如图所示,a、b、c、d为电场中的四点,c、d关于PQ连线的中垂线对称.一个离子从a运动到b(不计重力),轨迹如图所示,则下列判断正确的是( )
P、Q两电荷的电场线分布如图所示,a、b、c、d为电场中的四点,c、d关于PQ连线的中垂线对称.一个离子从a运动到b(不计重力),轨迹如图所示,则下列判断正确的是( )
 P、Q两电荷的电场线分布如图所示,a、b、c、d为电场中的四点,c、d关于PQ连线的中垂线对称.一个离子从a运动到b(不计重力),轨迹如图所示,则下列判断正确的是( )
P、Q两电荷的电场线分布如图所示,a、b、c、d为电场中的四点,c、d关于PQ连线的中垂线对称.一个离子从a运动到b(不计重力),轨迹如图所示,则下列判断正确的是( )| A. | P带负电 | B. | c、d两点的电场强度相同 | ||
| C. | 离子在运动过程中受到Q的吸引力 | D. | 离子从a到b,电势能增加 |
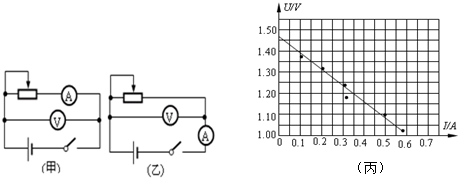
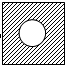 有一根细长而均匀的金属材料,长为l,电阻率为ρ,横戴面积外方(正方形)内圆,正方形边长为a,如图所示,现把它沿垂直纸面方向接入电路中,当电压为U时,电流为I,内圆的直径为多大?
有一根细长而均匀的金属材料,长为l,电阻率为ρ,横戴面积外方(正方形)内圆,正方形边长为a,如图所示,现把它沿垂直纸面方向接入电路中,当电压为U时,电流为I,内圆的直径为多大?