题目内容
15.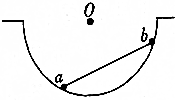 两个可视为质点的小球a和b,用质量可忽略不计、长度l=$\sqrt{2}$m的刚性细杆相连,放置在一个半径R=1m光滑的半球面内,如图所示.已知小球a的质量ma=2kg,小球b的质量mb=1kg.重力加速度g=10m/s2.求两小球平衡时细杆受到的压力大小.
两个可视为质点的小球a和b,用质量可忽略不计、长度l=$\sqrt{2}$m的刚性细杆相连,放置在一个半径R=1m光滑的半球面内,如图所示.已知小球a的质量ma=2kg,小球b的质量mb=1kg.重力加速度g=10m/s2.求两小球平衡时细杆受到的压力大小.
分析 对两个球分别受力分析,根据平衡条件作图后结合几何关系列式分析即可,注意杆对两个球的弹力大小相等、方向相反.
解答 解:对两个球受力分析如图所示:
由几何关系可知三角形Oab是等腰直角三角形,即∠Oab=∠Oba=45°,过圆心O作竖直线Oc交细杆于c点,设∠aOc=θ,则∠bOc=90°-θ;
由力的三角形定则和正弦定理可得:
$\frac{{m}_{a}g}{sin45°}=\frac{F}{sinθ}$,
$\frac{{{m_b}g}}{sin45°}=\frac{F}{sin(90°-θ)}$,
联立解得:F=4$\sqrt{10}$N;
由牛顿第三定律可知,细杆受到的压力等于细杆对球的弹力,即F′=F=4$\sqrt{10}$N.
答:两小球平衡时细杆受到的压力大小均为4$\sqrt{10}$N.
点评 本题的难点在于几何关系的确定,对学生的要求较点,只有找出合适的几何关系,才能找出突破本题的关键;应认真体会相似三角形及正弦定理的应用.难度教大.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
5.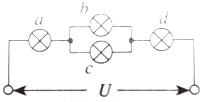 四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各灯泡的实际功率都没有超过它的额定功率.则下列这四盏灯实际消耗功率大小的说法正确的是( )
四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各灯泡的实际功率都没有超过它的额定功率.则下列这四盏灯实际消耗功率大小的说法正确的是( )
 四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各灯泡的实际功率都没有超过它的额定功率.则下列这四盏灯实际消耗功率大小的说法正确的是( )
四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各灯泡的实际功率都没有超过它的额定功率.则下列这四盏灯实际消耗功率大小的说法正确的是( )| A. | Pa>Pb+Pc+Pd | B. | Pa=Pc>Pb=Pd | C. | Pa>Pd>Pc>Pb | D. | Pd>Pb+Pc |
6.一带电体靠近一接地的空腔导体,空腔内无带电体,在静电平衡后下列物理量中等于零的有( )
| A. | 导体空腔内的电场强度 | B. | 导体外壳的带电量 | ||
| C. | 导体空腔内表面的带电量 | D. | 导体空腔内的电场线条数 |
3.下列说法中正确的是( )
| A. | 从甲物体自发传递热量给乙物体,说明甲物体的内能比乙物体多 | |
| B. | 热机的效率从原理上讲可达100% | |
| C. | 因为能量守恒,所以“能源危机”是不可能的 | |
| D. | 以上说法均不正确 |
10.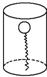 如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )
如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )
 如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )
如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )| A. | 自由落体运动 | B. | 向上升起一定高度后落下 | ||
| C. | 向下做加速度小于g的运动 | D. | 向下做加速度大于g的运动 |
20.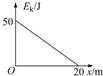 质量为1kg的物体以某一初速度在水平地面上滑行,由于受到地面摩擦阻力作用,其动能随位移变化的图线如图所示,g=10m/s2,则物体在水平地面上( )
质量为1kg的物体以某一初速度在水平地面上滑行,由于受到地面摩擦阻力作用,其动能随位移变化的图线如图所示,g=10m/s2,则物体在水平地面上( )
 质量为1kg的物体以某一初速度在水平地面上滑行,由于受到地面摩擦阻力作用,其动能随位移变化的图线如图所示,g=10m/s2,则物体在水平地面上( )
质量为1kg的物体以某一初速度在水平地面上滑行,由于受到地面摩擦阻力作用,其动能随位移变化的图线如图所示,g=10m/s2,则物体在水平地面上( )| A. | 所受合外力大小为5 N | B. | 滑行的总时间为4 s | ||
| C. | 滑行的加速度大小为1 m/s2 | D. | 滑行的加速度大小为2.5 m/s2 |
7.理想变压器连接电路如图甲所示,当输入电压波形如图乙时,已知原副线圈的匝数比为10:1,电流表读数为2A,则( )
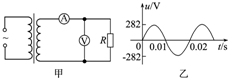

| A. | 电压表读数为282 V | B. | 电压表读数为28.2 V | ||
| C. | 输入功率为56.4 W | D. | 输入功率为40 W |
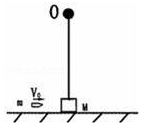 如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.
如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.