题目内容
2. 一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )| A. | $\frac{L_1}{2}\sqrt{\frac{g}{6h}}<v<{L_1}\sqrt{\frac{g}{6h}}$ | B. | $\frac{L_1}{4}\sqrt{\frac{g}{h}}<v<{L_1}\sqrt{\frac{(4L_1^2+L_2^2)g}{6h}}$ | ||
| C. | $\frac{L_1}{2}\sqrt{\frac{g}{6h}}<v<\frac{L_1}{2}\sqrt{\frac{(4L_1^2+L_2^2)g}{6h}}$ | D. | $\frac{L_1}{4}\sqrt{\frac{g}{h}}<v<\frac{1}{2}\sqrt{\frac{(4L_1^2+L_2^2)g}{6h}}$ |
分析 球要落在网右侧台面上,临界情况是与球网恰好不相撞,还有与球台边缘相碰,根据高度求出平抛运动的时间,根据几何关系求出最小的水平位移和最大的水平位移,从而得出最小速度和最大速度.
解答 解:若球与网恰好不相碰,根据3h-h=$\frac{1}{2}g{{t}_{1}}^{2}$得:${t}_{1}=\sqrt{\frac{4h}{g}}$,
水平位移的最小值为:${x}_{min}=\frac{{L}_{1}}{2}$,
则最小速度为:${v}_{1}=\frac{\frac{{L}_{1}}{2}}{{t}_{1}}=\frac{{L}_{1}}{4}\sqrt{\frac{g}{h}}$.
若球与球台边缘相碰,根据3h=$\frac{1}{2}g{{t}_{2}}^{2}$得:${t}_{2}=\sqrt{\frac{6h}{g}}$,
水平位移的最大值为:${x}_{max}=\sqrt{{{L}_{1}}^{2}+\frac{{{L}_{2}}^{2}}{4}}$,
则最大速度为:${v}_{2}=\frac{\sqrt{{{L}_{1}}^{2}+\frac{{{L}_{2}}^{2}}{4}}}{{t}_{2}}=\frac{1}{2}\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$,故D正确,A、B、C错误.
故选:D
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界情况,结合运动学公式灵活求解,难度中等.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
12. 在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时刻,波刚好传播到x=40m处,如图所示.则下列说法正确的是( )
在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时刻,波刚好传播到x=40m处,如图所示.则下列说法正确的是( )
 在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时刻,波刚好传播到x=40m处,如图所示.则下列说法正确的是( )
在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时刻,波刚好传播到x=40m处,如图所示.则下列说法正确的是( )| A. | 波源开始振动时方向沿y轴负方向 | |
| B. | t=0.15时,x=40m的质点位于平衡位置且向y轴正向运动 | |
| C. | t=0.15时,x=40m的质点位于平衡位置且向y轴负向运动 | |
| D. | t=0.15时,x=60m的质点刚好到达波峰 |
14.静止在地球上的物体都要随地球一起转动,a是位于赤道上的一点,b是位于北纬30°的一点,则下列说法正确的是( )
| A. | a、b两点的运动周期都相同 | B. | 它们的角速度是不同的 | ||
| C. | a、b两点的线速度大小相同 | D. | a、b两点线速度大小之比为2:$\sqrt{3}$ |
12.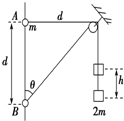 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法不正确的是(重力加速度为g)( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法不正确的是(重力加速度为g)( )
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法不正确的是(重力加速度为g)( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法不正确的是(重力加速度为g)( )| A. | 小环刚释放时轻绳中的张力一定大于2mg | |
| B. | 小环到达B处时,重物上升的高度约为($\sqrt{2}$-1)d | |
| C. | 小环在B处的速度与重物上升的速度大小之比等于$\frac{\sqrt{2}}{2}$ | |
| D. | 小环在B处的速度与重物上升的速度大小之比等于$\sqrt{2}$ |
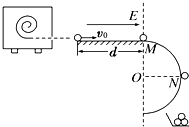 某塑料球成型机工作时,可以喷出速度v0=10m/s的塑料小球,已知喷出小球的质量m=1.0×10-4 kg,并且在喷出时已带了q=1.0×10-4 C的负电荷,如图所示,小球从喷口飞出后,先滑过长d=1.5m的水平光滑的绝缘轨道,而后又过半径R=0.4m的圆弧形竖立的光滑绝缘轨道.今在水平轨道上加上水平向右的电场强度为E的匀强电场,小球将恰好从圆弧轨道的最高点M处水平飞出;若再在圆形轨道区域加上垂直于纸面向里的匀强磁场后,小球将恰好从圆形轨道上与圆心等高的N点脱离轨道落入放在地面上接地良好的金属容器内,g=10m/s2,求:
某塑料球成型机工作时,可以喷出速度v0=10m/s的塑料小球,已知喷出小球的质量m=1.0×10-4 kg,并且在喷出时已带了q=1.0×10-4 C的负电荷,如图所示,小球从喷口飞出后,先滑过长d=1.5m的水平光滑的绝缘轨道,而后又过半径R=0.4m的圆弧形竖立的光滑绝缘轨道.今在水平轨道上加上水平向右的电场强度为E的匀强电场,小球将恰好从圆弧轨道的最高点M处水平飞出;若再在圆形轨道区域加上垂直于纸面向里的匀强磁场后,小球将恰好从圆形轨道上与圆心等高的N点脱离轨道落入放在地面上接地良好的金属容器内,g=10m/s2,求:
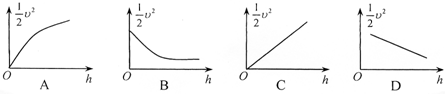
 起重机用恒力F使质量为1000kg的货物在1s内由静止上升了2m,则在这1s内,(不计空气阻力,g取10m/s2)
起重机用恒力F使质量为1000kg的货物在1s内由静止上升了2m,则在这1s内,(不计空气阻力,g取10m/s2) 一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线AB运动,如图,AB与电场线夹角θ=30°,已知带电微粒的质量m=1.0×10-7kg,电量q=1.0×10-10C,A、B相距L=20cm.(取g=10m/s2,结果保留二位有效数字)求:
一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线AB运动,如图,AB与电场线夹角θ=30°,已知带电微粒的质量m=1.0×10-7kg,电量q=1.0×10-10C,A、B相距L=20cm.(取g=10m/s2,结果保留二位有效数字)求: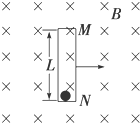 如图所示,在空间有水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向里.在磁场中有一长为L、内壁光滑且绝缘的细筒MN竖直放置,筒的底部有一电荷量为+q的小球,现使细筒MN沿垂直于磁场方向水平向右匀速运动,设小球带电量不变.
如图所示,在空间有水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向里.在磁场中有一长为L、内壁光滑且绝缘的细筒MN竖直放置,筒的底部有一电荷量为+q的小球,现使细筒MN沿垂直于磁场方向水平向右匀速运动,设小球带电量不变.