��Ŀ����
10������֤��е���غ㶨�ɵ�ʵ������1������˵������ȷ����AB��
A���ڰ�װ���ʱ��ʱ��ī��ֽ��Ҫ��������ֽ��֮��
B��Ϊ�˼�С����������Ӧ��Щ
C��ʵ��ʱ��Ӧ���ɿ�ֽ�����ش��˶��ȶ����ٽ�ͨ��Դ
D����tΪ��㵽ij���ʱ�䣬����õ���ٶȿ��ù�ʽv=gt
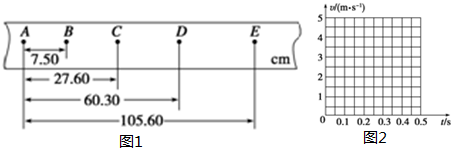
��2����ʵ�������õ��ش�������Ϊm=0.1kg�����ֽ����ͼ��ʾ�����ʱ����Ϊ0.02s��ȡB��������ش�����EkB=0.0171J���ӿ�ʼ��������B��ʱ�ش����������ܼ�������0.0172J����������������λ��Ч���֣�

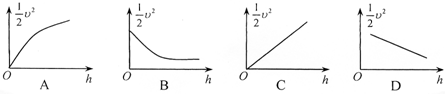
��3������ֽ�������ظ�����ٶ�v��������Ӧ����ľ���h������$\frac{1}{2}{v^2}$Ϊ���ᡢ��hΪ����������ͼ��Ӧ����ͼ�е�C��
���� ���ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ���������������������ݴ����Լ�ע����������ʵ��������Դ��
ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȣ��Ӷ�������ܣ����ݹ��ܹ�ϵ���������ܼ�С������������������ֵ��
��� �⣺��1��A���ڰ�װ���ʱ��ʱ��ī��ֽ��Ҫ��������ֽ��֮�䣬��A��ȷ��
B��Ϊ�˼�С����������Ӧ��Щ�����Ӧ��СЩ����B��ȷ��
C��ʵ��ʱ��Ӧ�Ƚ�ͨ��Դ�����ɿ�ֽ������C����
D������������ʵ���˶��������������˶�����������������Ĺ�������ٶȣ���ô�Ͳ���Ҫ��֤����D����
��2�������ȱ���ֱ���˶���ʱ���е��˲ʱ�ٶȵ��ڸù����е�ƽ���ٶ��У�
vB=$\frac{{x}_{AC}}{2T}$=$\frac{0.0312-0.0078}{2��0.02}$=0.59m/s
�����䶯��Ϊ��EkB=$\frac{1}{2}$m${v}_{B}^{2}$=$\frac{1}{2}$��0.1����0.59��2=0.0171J
�������������������ܵļ�С��������У�
��EP=mgx=0.1��9.8��0.0176=0.0172J
��3������$\frac{1}{2}$v2-hͼ�ߴ������ݣ������۽Ƕ�����������������л�е���غ���Եó���
mgh=$\frac{1}{2}$mv2����$\frac{1}{2}$v2=gh
������$\frac{1}{2}$v2Ϊ���ᣬ��hΪ���ử����ͼ��Ӧ�ǹ�ԭ�����бֱ�ߣ�Ҳ����ͼ�е�C��
�ʴ�Ϊ����1��AB�� ��2��0.0171�� 0.0172����3��C��
���� ��ȷ���ʵ�������ǰ������ȷʵ��ԭ������ʵ��ԭ���������з�������ʵ�����ġ��������ݡ��������ȣ������°빦����Ч����
���˶�ѧ��ʽ�����ۺͶ��ܡ��������ܵĶ���ʽ��������Ǹ�ʵ��ij������⣬Ҫע�ⵥλ�Ļ������Ч���ֵı�����

 �Ķ��쳵ϵ�д�
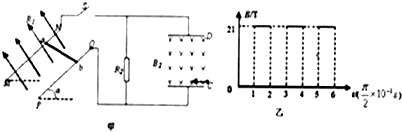
�Ķ��쳵ϵ�д� һ������ˮƽ�����ϣ��ܵ�һˮƽ����F�����ã�F�Ĵ�С��ʱ��t�Ĺ�ϵ��ͼ����ʾ������˶����ٶ�v-tͼ����ͼ����ʾ��6s����ٶ�ͼ��û�л�����gȡ10m/s2������˵����ȷ���ǣ�������
һ������ˮƽ�����ϣ��ܵ�һˮƽ����F�����ã�F�Ĵ�С��ʱ��t�Ĺ�ϵ��ͼ����ʾ������˶����ٶ�v-tͼ����ͼ����ʾ��6s����ٶ�ͼ��û�л�����gȡ10m/s2������˵����ȷ���ǣ�������| A�� | ��黬��ʱ�ܵ�Ħ������С��6N | |
| B�� | ��������Ϊ2kg | |
| C�� | �����6��9s�ڵļ��ٶȴ�С��1m/s2 | |
| D�� | �����9s�ڵ�ƽ���ٶȴ�С��4m/s |
 һ����ƹ���������ƹ����̨��ͼ��ʾ��ˮƽ̨��ij��Ϳ��ֱ�ΪL1��L2���м������߶�Ϊh���������װ��̨������Ե���е㣬���Բ�ͬ�������Ҳͬ����ˮƽ����ƹ��������̨��߶�Ϊ3h�����ƿ��������ã��������ٶȴ�СΪg����ƹ����ķ�������v��ij��Χ�ڣ�ͨ��ѡ����ʵķ�����ʹƹ�����䵽�����Ҳ�̨���ϣ���v�����ȡֵ��Χ�ǣ�������
һ����ƹ���������ƹ����̨��ͼ��ʾ��ˮƽ̨��ij��Ϳ��ֱ�ΪL1��L2���м������߶�Ϊh���������װ��̨������Ե���е㣬���Բ�ͬ�������Ҳͬ����ˮƽ����ƹ��������̨��߶�Ϊ3h�����ƿ��������ã��������ٶȴ�СΪg����ƹ����ķ�������v��ij��Χ�ڣ�ͨ��ѡ����ʵķ�����ʹƹ�����䵽�����Ҳ�̨���ϣ���v�����ȡֵ��Χ�ǣ�������| A�� | $\frac{L_1}{2}\sqrt{\frac{g}{6h}}��v��{L_1}\sqrt{\frac{g}{6h}}$ | B�� | $\frac{L_1}{4}\sqrt{\frac{g}{h}}��v��{L_1}\sqrt{\frac{��4L_1^2+L_2^2��g}{6h}}$ | ||
| C�� | $\frac{L_1}{2}\sqrt{\frac{g}{6h}}��v��\frac{L_1}{2}\sqrt{\frac{��4L_1^2+L_2^2��g}{6h}}$ | D�� | $\frac{L_1}{4}\sqrt{\frac{g}{h}}��v��\frac{1}{2}\sqrt{\frac{��4L_1^2+L_2^2��g}{6h}}$ |
 ijͬѧ����ħ��ʱ����һС�����δ��������Լ��������Ȼ�����һ���ҵĽ���С��ָ�ֻ��ţ����С����������Ĺ�����Ʈ�����������赱���ص�С����λ��С������Ϸ�ijһλ��C��ͼ�Ц�=37�㣩ʱ������С��ƫ����ֱ����ļн�Ҳ��37�㣬��ͼ��ʾ����֪С�������Ϊm=4.8Kg����ͬѧ����������������ΪM=50Kg�����ʱ��
ijͬѧ����ħ��ʱ����һС�����δ��������Լ��������Ȼ�����һ���ҵĽ���С��ָ�ֻ��ţ����С����������Ĺ�����Ʈ�����������赱���ص�С����λ��С������Ϸ�ijһλ��C��ͼ�Ц�=37�㣩ʱ������С��ƫ����ֱ����ļн�Ҳ��37�㣬��ͼ��ʾ����֪С�������Ϊm=4.8Kg����ͬѧ����������������ΪM=50Kg�����ʱ��