题目内容
13.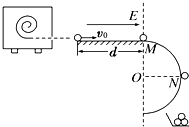 某塑料球成型机工作时,可以喷出速度v0=10m/s的塑料小球,已知喷出小球的质量m=1.0×10-4 kg,并且在喷出时已带了q=1.0×10-4 C的负电荷,如图所示,小球从喷口飞出后,先滑过长d=1.5m的水平光滑的绝缘轨道,而后又过半径R=0.4m的圆弧形竖立的光滑绝缘轨道.今在水平轨道上加上水平向右的电场强度为E的匀强电场,小球将恰好从圆弧轨道的最高点M处水平飞出;若再在圆形轨道区域加上垂直于纸面向里的匀强磁场后,小球将恰好从圆形轨道上与圆心等高的N点脱离轨道落入放在地面上接地良好的金属容器内,g=10m/s2,求:
某塑料球成型机工作时,可以喷出速度v0=10m/s的塑料小球,已知喷出小球的质量m=1.0×10-4 kg,并且在喷出时已带了q=1.0×10-4 C的负电荷,如图所示,小球从喷口飞出后,先滑过长d=1.5m的水平光滑的绝缘轨道,而后又过半径R=0.4m的圆弧形竖立的光滑绝缘轨道.今在水平轨道上加上水平向右的电场强度为E的匀强电场,小球将恰好从圆弧轨道的最高点M处水平飞出;若再在圆形轨道区域加上垂直于纸面向里的匀强磁场后,小球将恰好从圆形轨道上与圆心等高的N点脱离轨道落入放在地面上接地良好的金属容器内,g=10m/s2,求:(1)所加电场的电场强度E;
(2)所加磁场的磁感应强度B.
分析 (1)在水平轨道上加上水平向右的电场强度为E的匀强电场,小球将恰好从圆弧轨道的最高点M处水平飞出,知支持力为零,小球所受的重力提供向心力,对水平轨道段运用动能定理,求出所加电场的电场强度E.
(2)在圆形轨道区域加上垂直于纸面向里的匀强磁场后,小球将恰好从圆形轨道上与圆心等高的N点脱离轨道,知在N点轨道对球的弹力为零,小球所受的洛伦兹力提供向心力,在M到N端,只有重力做功,机械能守恒,根据机械能守恒定律求出所加磁场的磁感应强度.
解答 解:(1)设小球在M点的速率为v1,只加电场时对小球在M点,
由牛顿第二定律得:mg=m$\frac{{v}_{1}^{2}}{R}$,
在水平轨道上,对小球由动能定理得:
qEd=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02,
解得:E=32V/m;
(2)设小球在N点速率为v2,在N点,
由牛顿第二定律得:qv2B=m$\frac{{v}_{2}^{2}}{R}$,
从M到N点,由机械能守恒定律得:
mgR+$\frac{1}{2}$mv12=$\frac{1}{2}$mv22,解得:B=5$\sqrt{3}$T.
答:(1)所加电场的电场强度E为32V/m;
(2)所加磁场的磁感应强度B为5$\sqrt{3}$T.
点评 本题综合运用了动能定理、机械能守恒定律、牛顿第二定律,并与电场磁场相结合,关键在于合理地选择研究的过程,并能正确地进行受力分析;解决本题的关键是抓住小球在M点恰好水平飞出所隐含的速度条件以及恰好从N点脱离轨道所隐含的速度条件.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2. 一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
 一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )| A. | $\frac{L_1}{2}\sqrt{\frac{g}{6h}}<v<{L_1}\sqrt{\frac{g}{6h}}$ | B. | $\frac{L_1}{4}\sqrt{\frac{g}{h}}<v<{L_1}\sqrt{\frac{(4L_1^2+L_2^2)g}{6h}}$ | ||
| C. | $\frac{L_1}{2}\sqrt{\frac{g}{6h}}<v<\frac{L_1}{2}\sqrt{\frac{(4L_1^2+L_2^2)g}{6h}}$ | D. | $\frac{L_1}{4}\sqrt{\frac{g}{h}}<v<\frac{1}{2}\sqrt{\frac{(4L_1^2+L_2^2)g}{6h}}$ |

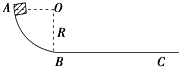 如图所示,物体从半径为R的光滑$\frac{1}{4}$竖直圆弧轨道顶端由静止下滑后,在粗糙水平面上又滑行一段距离BC=x停止,图中OA线水平,OB线竖直,O是圆心,问:
如图所示,物体从半径为R的光滑$\frac{1}{4}$竖直圆弧轨道顶端由静止下滑后,在粗糙水平面上又滑行一段距离BC=x停止,图中OA线水平,OB线竖直,O是圆心,问: