题目内容
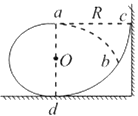
【题目】如图所示，半径为R的1/4固定圆弧轨道竖直放置，下端与水平地面在P点相切，水平地面上静止一质量为m2＝2m的物体，其左端固定有劲度系数为k的轻弹簧，Q点为弹簧处于原长时的左端点，已知PQ＝R，物块与水平地面PQ间的动摩擦因数为＝0.4，Q点右侧光滑。现有一质量为m1＝m的物块（可视为质点）从圆弧轨道的最高点由静止开始下滑，当m2固定时，m1向右运动压缩弹簧后被弹簧弹回．向左运动停止在PQ的中点，已知重力加速度为g。
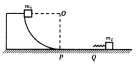
（1）求m1从圆弧轨道上下滑过程中克服摩擦力所做的功；
（2）m2不固定时．求弹簧的最大弹性势能；
（3）求m2不固定时，m1最终停止的位置。
【答案】（1）
（2）
（3）Q点左侧
处
【解析】本题考查物体沿在粗糙曲面和粗糙水平面的运动及物体间的弹性碰撞。需应用动能定理，弹性碰撞中的动量守恒和动能守恒等知识综合求解。
（1）设m1从圆弧轨道上下滑过程中克服摩擦力所做的功
，对m1从开始下滑到停止的过程应用动能定理得
解得m1从圆弧轨道上下滑过程中克服摩擦力所做的功
（2）设m1从圆弧轨道由静止下滑至Q点时速度为v0, 由动能定理得
，解得： 
当弹簧有最大弹性势能时，m1和m2具有相同速度，设为v，则有
解得弹簧的最大弹性势能
（3）设m1与弹簧分离时，m1和m2的速度分别为v1和v2, 则有
解得： 
负号表示方向向左
设m1最终停在Q点左侧x处，由动能定理得
解得
，即m1最终停在Q点左侧
处
练习册系列答案
相关题目
