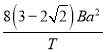题目内容
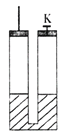
【题目】如图所示，在电场强度大小为
、方向竖直向上的匀强电场中，长为L的绝缘轻绳一端固定在O点，另一端固定一质量为m、带电荷量为＋q的直放置且尺寸较小．现将小球拉到与O点同一高度且距O点右侧L处的C点，给它一个竖直向上的初速度v0，此后小球在A、B右侧区域竖直平面内做圆周运动，并不时与挡板A、B碰撞，小球每次与挡板碰撞时均不损失机械能，碰后瞬间电场均立即反向，但大小不变．重力加速度大小为g．
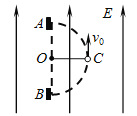
(1)若小球与挡板A碰后，能做圆周运动到挡板B，求初速度v0的最小值；
(2)若小球的初速度为(1)中的最小值，求小球与B第1次碰撞前瞬间，轻绳拉力的大小；
(3)若小球的初速度为(1)中的最小值，且轻绳承受的最大拉力为50mg，在轻绳断前，小球与挡板总共碰撞的次数为多少？
【答案】(1) 
(2)12mg (3)11
【解析】(1)小球与挡板A碰前，由于qE＝mg，小球将做匀速圆周运动到挡板A.
小球与挡板A碰后，电场立即反向，小球在电场力和重力作用下做圆周运动到挡板B，此过程中F＝qE＋mg＝2mg，方向向下
要能做圆周运动，则最高点A处满足： 
解得： 
因而小球初速度的最小值为
.
(2)小球第1次与挡板A碰后，将做变速圆周运动到挡板B与挡板B第1次碰撞，在该过程中，根据动能定理有： 
第1次与B碰前瞬间，根据牛顿第二定律有： 
解得： 
(3)根据题设分析，小球每次向上做圆周运动时，均有qE＝mg，且方向相反，向下做圆周运动时，也有qE＝mg，但方向相同．所以小球每次向上均做匀速圆周运动，向下均做变速圆周运动，因此轻绳断裂只能发生在小球向下运动的过程中．
第2次与A碰后 
，其中
第2次与B碰前瞬间，根据牛顿第二定律有： 
解得： 
由以上分析可知，小球每次与挡板B碰撞前瞬间，轻绳的拉力均比上一次碰撞前瞬间增加
因而小球与挡板B第n次碰前瞬间
轻绳的拉力为
如果轻绳断裂，则应有： 
解得： 
因而小球与挡板A碰撞6次，与挡板B碰撞5次后在小球还未与挡板B发生第6次碰撞前轻绳已经断裂，因而小球与挡板碰撞的
总次数为：N＝6＋5＝11(次)．
