题目内容
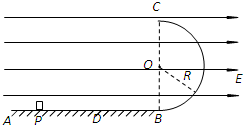
如图所示,间距为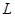 、半径为
、半径为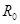 的内壁光滑的
的内壁光滑的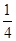 圆弧固定轨道,右端通过导线接有阻值为
圆弧固定轨道,右端通过导线接有阻值为 的电阻,圆弧轨道处于竖直向上的匀强磁场中,磁场的磁感应强度为
的电阻,圆弧轨道处于竖直向上的匀强磁场中,磁场的磁感应强度为 。质量为
。质量为 、电阻为
、电阻为 、长度也为
、长度也为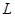 的金属棒,从与圆心等高的
的金属棒,从与圆心等高的 处由静止开始下滑,到达底端
处由静止开始下滑,到达底端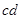 时,对轨道的压力恰好等于金属棒的重力2倍,不计导轨和导线的电阻,空气阻力忽略不计,重力加速度为
时,对轨道的压力恰好等于金属棒的重力2倍,不计导轨和导线的电阻,空气阻力忽略不计,重力加速度为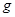 。求:
。求: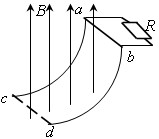
(1)金属棒到达底端时,电阻 两端的电压
两端的电压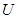 多大;
多大;
(2)金属棒从 处由静止开始下滑,到达底端
处由静止开始下滑,到达底端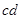 的过程中,通过电阻
的过程中,通过电阻 的电量
的电量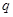 ;
;
(3)用外力将金属棒以恒定的速率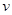 从轨道的低端
从轨道的低端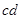 拉回与圆心等高的
拉回与圆心等高的 处的过程中,电阻
处的过程中,电阻 产生的热量
产生的热量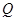 。
。
(1)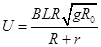 (2)
(2) (3)
(3)
解析试题分析:(1)金属棒滑到轨道最低点时,根据牛顿定律有 ①
①
根据题意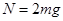 ②
②
金属棒切割磁感线产生的电动势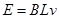 ③
③
金属棒产生的感应电流  ④
④
电阻 两端的电压
两端的电压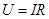 ⑤
⑤
由方程①②③④⑤式解得 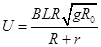 ⑥
⑥
(2)金属棒从ab处由静止开始下滑,到达底端cd的过程中,通过电阻R的电量: ⑦
⑦
根据欧姆定律有: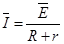 ⑧
⑧
根据法拉第电磁感应定律有: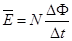 ⑨
⑨
线框进入磁场过程中磁通量的变化量: ⑩
⑩
由以上各式解得: ⑾
⑾
(3)金属棒以恒定的速率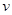 从轨道的低端
从轨道的低端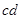 拉回与圆心等高的
拉回与圆心等高的 处的过程中,金属棒垂直于磁场方向的速度
处的过程中,金属棒垂直于磁场方向的速度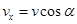 ⑿
⑿
金属棒切割产生的电动势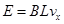 ⒀
⒀
电路中的电流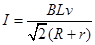 ⒁
⒁
金属棒运动的时间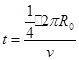 ⒂
⒂
金属棒产生的热量 ⒃
⒃
解得  ⒄
⒄
评分标准:本题16分。第一问共5分,其中①③④⑤⑥式每式各1分;第二问共计5分,其中⑦⑧⑨⑩⑾式每式各1分。第三问共计6分。其中⑿⒀⒁⒂⒃⒄式每式各1分。
考点:本题考查电磁感应的综合问题。

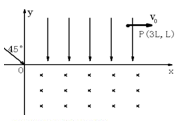
 沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角
沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角 ,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小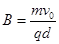 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
 ,虚线下方匀强磁场范围足够大,磁感应强度为
,虚线下方匀强磁场范围足够大,磁感应强度为 ,现有质量为
,现有质量为 、电量为
、电量为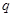 的带正电粒子从距电磁场边界
的带正电粒子从距电磁场边界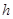 处无初速释放(带电粒子重力可忽略不计).求:
处无初速释放(带电粒子重力可忽略不计).求: 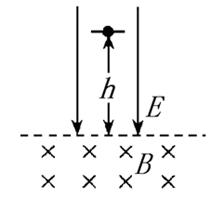
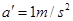 =45°。求:
=45°。求: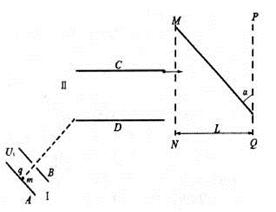
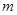 、带电量为
、带电量为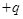 的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。
的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。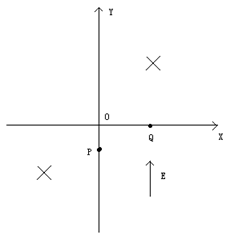
 平面第一象限整个区域分布匀强电场,电场方向平行
平面第一象限整个区域分布匀强电场,电场方向平行 轴向下,在第四象限内存在有界匀强磁场,左边界为
轴向下,在第四象限内存在有界匀强磁场,左边界为 的直线,磁场方向垂直纸面向外。质量为
的直线,磁场方向垂直纸面向外。质量为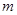 、带电量为
、带电量为 的粒子从
的粒子从 点以初速度
点以初速度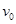 垂直
垂直 轴上
轴上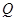 点以与
点以与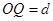 ,不计粒子重力。求:
,不计粒子重力。求:
 的取值范围;
的取值范围; 的电阻。在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T。一根质量m=0.10kg的直金属杆
的电阻。在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T。一根质量m=0.10kg的直金属杆 垂直于轨道放在两根轨道上。某时刻杆
垂直于轨道放在两根轨道上。某时刻杆 =2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以
=2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以 =2.0m/s2的加速度做匀减速直线运动。杆
=2.0m/s2的加速度做匀减速直线运动。杆
 时,水平拉力的大小;
时,水平拉力的大小;