题目内容
（12分）如图所示，水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×104N/C。现有一电荷量q=+1.0×10 4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能够通过最高点C,已知带电体与水平轨道间的动摩擦因数μ=0.50，重力加速度g=10m/s2。求：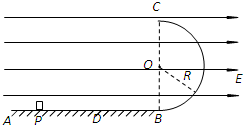 
（1）带电体运动到圆形轨道的最低点B时，圆形轨道对带电体支持力的大小；
（2）带电体在水平轨道上的释放点P到B点的距离；
（3）带电体第一次经过C点后，落在水平轨道上的位置到B点的距离。
（1）6N；（2）2m；（3）
解析试题分析：（1）设带电体通过C点时的速度为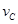
，根据牛顿第二定律
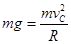（1分）
设带电体通过B点时的速度为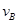
，设轨道对带电体的支持力大小为
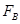，带电体地B点时。
根据牛顿第二定律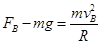
（1分）
带电体从B运动到C过程中，根据动能定理：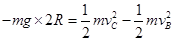
（2分）
联立解得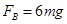
=6N （1分）
（2）设PB间的距离为S ,则：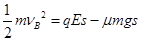
（2分）
解得：s=2m （1分）
（3）设带电体从最高点C落至水平轨道上的d点经历时间为t，根据运动的分解有：
竖直方向：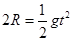
（1分）
水平方向：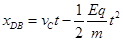
（2分）
联立得
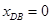（1分）
考点：动能定理，牛顿第二定律，平抛运动
练习册系列答案
相关题目
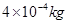带电量为q=+
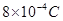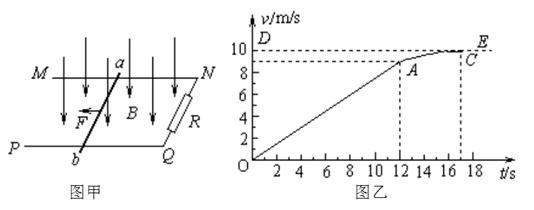
的带电小球，从小孔P以速度v=2m/s水平射入上述电场、磁场区域，之后从OA板上的M点垂直OA方向飞出上述的电磁场区域后而进入下方的电磁场区域 ，OA板下方电场方向变为水平向右，电场强度大小为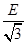
，当小球碰到水平地面时立刻加上匀强磁场，磁感应强度大小仍为B=1T，方向垂直纸面向里。小球与水平地面相碰时，竖直方向速度立刻减为零，水平方向速度不变，小球运动到D处刚好离开水平地面，然后沿着曲线DQ运动，重力加速度为g=10m/s2，小球在水平地面上运动过程中电量保持不变，不计摩擦。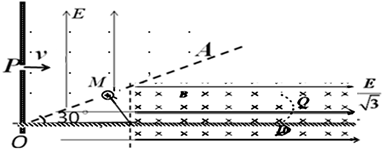
；
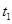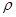（即把那一段曲线尽可能的微分，近似一个圆弧，这个圆弧对应的半径即曲线上这个点的曲率半径）。求vm与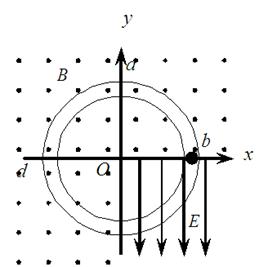
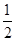，在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，MN为电场的理想边界，场强大小为E1 ，ON="d" 。在第二象限内充满一个沿x轴负方向的匀强电场，场强大小为E2。电子从y轴上的A点以初速度
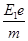沿x轴负方向射入第二象限区域，它到达的最右端为图中的B点，之后返回第一象限，且从MN上的P点离开。已知A点坐标为（0，h）．电子的电量为e，质量为m，电子的重力忽略不计，求：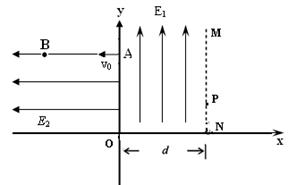
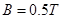×105N/C的匀强电场，其方向与y轴正方向成60o角且指向左上方，一重力不计的带正电粒子，从坐标原点O沿x轴正方向进入磁场，已知粒子的比荷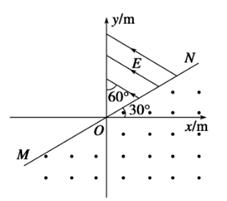
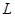、半径为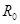
的内壁光滑的
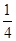圆弧固定轨道，右端通过导线接有阻值为
的电阻，圆弧轨道处于竖直向上的匀强磁场中，磁场的磁感应强度为
。质量为
、电阻为
、长度也为
处由静止开始下滑，到达底端
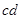时，对轨道的压力恰好等于金属棒的重力2倍，不计导轨和导线的电阻，空气阻力忽略不计，重力加速度为
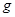。求：
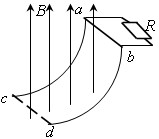
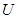多大；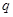
；
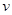从轨道的低端
。