题目内容
13.一号卫星和二号卫星分别绕地球做匀速圆周运动,它们的质量之比为1:3,它们的轨道半径之比为1:4,则:(1)一号卫星和二号卫星的线速度之比为多少?
(2)一号卫星和二号卫星的周期之比为多少?
(3)一号卫星和二号卫星的向心加速度之比为多少?
分析 根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}}{{T}^{2}}r$,解出线速度v、周期T向心加速度a与轨道半径r之间的关系表达式,根据半径关系求其比值.
解答 解:根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}}{{T}^{2}}r$=ma,得$v=\sqrt{\frac{GM}{r}}$,$T=2π\sqrt{\frac{{r}^{3}}{GM}}$,
(1)$\frac{{v}_{1}}{{v}_{2}}=\sqrt{\frac{{r}_{2}}{{r}_{1}}}=\sqrt{\frac{4}{1}}=\frac{2}{1}$
(2)$\frac{{T}_{1}}{{T}_{2}}=\sqrt{{(\frac{{r}_{1}}{{r}_{2}})}^{3}}=\sqrt{{(\frac{1}{4})}^{3}}=\frac{1}{8}$
(3)向心加速度:a=$\frac{GM}{{r}^{2}}$
所以:$\frac{{a}_{1}}{{a}_{2}}=\frac{{r}_{2}^{2}}{{r}_{1}^{2}}=\frac{16}{1}$
答:(1)一号卫星和二号卫星的线速度之比为2:1;
(2)一号卫星和二号卫星的周期之比为1:8;
(3)一号卫星和二号卫星的向心加速度之比为16:1.
点评 本题关键是要掌握万有引力提供向心力这个关系,能够根据题意选择恰当的向心力的表达式.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
3. 如图所示,倾角θ=30°的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接滑轮的轻杆沿竖直方向,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,已知C的质量为2m,A、B质量均为m,则下列说法正确的是( )
如图所示,倾角θ=30°的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接滑轮的轻杆沿竖直方向,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,已知C的质量为2m,A、B质量均为m,则下列说法正确的是( )
 如图所示,倾角θ=30°的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接滑轮的轻杆沿竖直方向,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,已知C的质量为2m,A、B质量均为m,则下列说法正确的是( )
如图所示,倾角θ=30°的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接滑轮的轻杆沿竖直方向,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,已知C的质量为2m,A、B质量均为m,则下列说法正确的是( )| A. | 定滑轮受到轻杆的作用力为$\sqrt{3}$mg | B. | C受到水平面的摩擦力为mg | ||
| C. | B受到C间摩擦力大小为$\frac{1}{2}$mg | D. | 水平面对C的支持力为$\frac{5}{2}$mg |
4.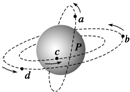 a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d均为同步卫星,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示.下列说法中正确的是( )
a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d均为同步卫星,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示.下列说法中正确的是( )
 a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d均为同步卫星,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示.下列说法中正确的是( )
a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d均为同步卫星,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示.下列说法中正确的是( )| A. | a、c的加速度大小相等,且小于b的加速度 | |
| B. | a、c的线速度大小相等,且大于第一宇宙速度 | |
| C. | b、d的角速度大小相等,且小于a的角速度 | |
| D. | a、c存在在P点相撞的危险 |
1. 如图所示,一块质量为M的木板B在光滑的水平桌面上以速度v0匀速向右滑行,某时刻把一质量为m的小铁块A(初速度为零)放在B的右端,它将在B上滑行一段距离L后与B相对静止达到共同速度v,此时木板B前进距离x,若小铁块和木板间的动摩擦因数为μ.下列说法正确的是( )
如图所示,一块质量为M的木板B在光滑的水平桌面上以速度v0匀速向右滑行,某时刻把一质量为m的小铁块A(初速度为零)放在B的右端,它将在B上滑行一段距离L后与B相对静止达到共同速度v,此时木板B前进距离x,若小铁块和木板间的动摩擦因数为μ.下列说法正确的是( )
 如图所示,一块质量为M的木板B在光滑的水平桌面上以速度v0匀速向右滑行,某时刻把一质量为m的小铁块A(初速度为零)放在B的右端,它将在B上滑行一段距离L后与B相对静止达到共同速度v,此时木板B前进距离x,若小铁块和木板间的动摩擦因数为μ.下列说法正确的是( )
如图所示,一块质量为M的木板B在光滑的水平桌面上以速度v0匀速向右滑行,某时刻把一质量为m的小铁块A(初速度为零)放在B的右端,它将在B上滑行一段距离L后与B相对静止达到共同速度v,此时木板B前进距离x,若小铁块和木板间的动摩擦因数为μ.下列说法正确的是( )| A. | 木板对铁块的摩擦力对铁块做的功等于μmgL | |
| B. | 木板克服摩擦力做的功等于μmgL | |
| C. | 系统产生的内能等于μmgL | |
| D. | 系统产生的内能等于$\frac{1}{2}$Mv${\;}_{0}^{2}$-$\frac{1}{2}$(M+m)v2 |
8.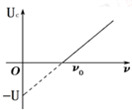 某种金属在光的照射下产生光电效应,其遏止电压Uc与入射光频率v的关系图象如图所示.则由图象可知( )
某种金属在光的照射下产生光电效应,其遏止电压Uc与入射光频率v的关系图象如图所示.则由图象可知( )
 某种金属在光的照射下产生光电效应,其遏止电压Uc与入射光频率v的关系图象如图所示.则由图象可知( )
某种金属在光的照射下产生光电效应,其遏止电压Uc与入射光频率v的关系图象如图所示.则由图象可知( )| A. | 任何频率的入射光都能产生光电效应 | |
| B. | 该金属的逸出功等于hv0 | |
| C. | 入射光的频率为3v0时,产生的光电子的最大初动能为2hv0 | |
| D. | 若已知电子电量e,就可以求出普朗克常量h | |
| E. | 入射光的频率发生变化时,遏止电压不变 |
5.在图中,甲、乙两图分别为测灯泡电阻R的电路图,下述说法正确的是( )
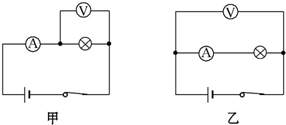

| A. | 甲图的接法叫电流表外接法,乙图的接法叫电流表的内接法 | |
| B. | 甲中R测>R真,乙中R测<R真 | |
| C. | 甲中误差由电压表分流引起,为了减小误差,就使R?RV,故此法测较小电阻好 | |
| D. | 乙中误差由电流表分压引起,为了减小误差,应使R?RA,故此法测较大电阻好 |
3. 如图所示,把一个带正电的小球放入原来不带电的金属空腔球壳内并接触,其结果可能是( )
如图所示,把一个带正电的小球放入原来不带电的金属空腔球壳内并接触,其结果可能是( )
 如图所示,把一个带正电的小球放入原来不带电的金属空腔球壳内并接触,其结果可能是( )
如图所示,把一个带正电的小球放入原来不带电的金属空腔球壳内并接触,其结果可能是( )| A. | 球壳的内、外表面都带正电 | |
| B. | 只有球壳外表面带正电 | |
| C. | 球壳的内表面带正电,外表面带负电 | |
| D. | 球壳的内表面带负电,外表面带正电 |
