题目内容
4.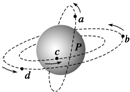 a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d均为同步卫星,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示.下列说法中正确的是( )
a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d均为同步卫星,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示.下列说法中正确的是( )| A. | a、c的加速度大小相等,且小于b的加速度 | |
| B. | a、c的线速度大小相等,且大于第一宇宙速度 | |
| C. | b、d的角速度大小相等,且小于a的角速度 | |
| D. | a、c存在在P点相撞的危险 |
分析 卫星绕地球做圆周运动,万有引力提供向心力,应用万有引力公式与牛顿第二定律求出加速度、角速度、线速度,然后分析答题.
解答 解:A、人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,
根据万有引力提供向心力为:
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}=m\frac{{v}^{2}}{r}$=mω2r=ma,
解得:v=$\sqrt{\frac{GM}{r}}$①,ω=$\sqrt{\frac{GM}{{r}^{3}}}$ ②,a=$\frac{GM}{{r}^{2}}$③
A、a、c两颗卫星的轨道半径相同,且小于b卫星的轨道半径,根据③式,a、c的加速度大小相等,且大于b的加速度,故A错误;
B、a、c两颗卫星的轨道半径相同,且小于d卫星的轨道半径,根据①式,a、c的线速度大小相等,且小于第一宇宙速度,故B错误;
C、b、d两颗卫星的轨道半径相同,且大于a卫星的轨道半径,根据②式b、d的角速度大小相等,且小于a的角速度,故C正确;
D、根据②式,可知a与c的角速度相等,则周期相等,若题目开始时不相碰,则以后也不会相碰,故D错误;
故选:C
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度、角速度和加速度的表达式,再进行讨论;除向心力外,线速度、角速度、周期和加速度均与卫星的质量无关,只与轨道半径有关.

练习册系列答案
相关题目
14.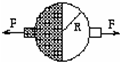 如图所示,两个半球拼成的球形容器,内部被抽成真空,球形容器半径为R,大气压强为P,要使两半球分开两侧拉力至少为( )
如图所示,两个半球拼成的球形容器,内部被抽成真空,球形容器半径为R,大气压强为P,要使两半球分开两侧拉力至少为( )
 如图所示,两个半球拼成的球形容器,内部被抽成真空,球形容器半径为R,大气压强为P,要使两半球分开两侧拉力至少为( )
如图所示,两个半球拼成的球形容器,内部被抽成真空,球形容器半径为R,大气压强为P,要使两半球分开两侧拉力至少为( )| A. | 4πR2P | B. | 2πR2P | C. | πR2P | D. | $\frac{π{R}^{2}P}{2}$ |
15.下列说法正确的是( )
| A. | 升国旗时,观察到国旗冉冉升起,观察者是以地面或旗杆作为参考系的 | |
| B. | 某同学参加学校田径运动会200m决赛中的位移大小等于路程 | |
| C. | 某中学每天早上开始上课时间是8:00指的是时间 | |
| D. | 矢量都是有方向的,初中学过的电流是有方向的量,所以电流是矢量 |
19. 如图所示,一根轻弹簧下端固定,竖直立在水平面上,上端放一只小球,用力F将小
如图所示,一根轻弹簧下端固定,竖直立在水平面上,上端放一只小球,用力F将小
球缓慢地压到D点静止,弹簧始终处于弹性限度内.突然撤去力F,小球从静止开始
向上运动,B点是弹簧原长时上端的位置,在C位置时小球所受弹力大小等于重力,
在A位置时小球的速度为零.小球运动过程中,下列说法中正确的是( )
 如图所示,一根轻弹簧下端固定,竖直立在水平面上,上端放一只小球,用力F将小
如图所示,一根轻弹簧下端固定,竖直立在水平面上,上端放一只小球,用力F将小球缓慢地压到D点静止,弹簧始终处于弹性限度内.突然撤去力F,小球从静止开始
向上运动,B点是弹簧原长时上端的位置,在C位置时小球所受弹力大小等于重力,
在A位置时小球的速度为零.小球运动过程中,下列说法中正确的是( )
| A. | 在B位置小球动能最大 | |
| B. | D→B位置小球加速度一直减少 | |
| C. | C→A位置小球重力势能的增加等于小球动能的减少 | |
| D. | D→A位置小球重力势能的增加等于弹簧弹性势能的减少 |
9. 如图所示,A、B两个点电荷在真空中所产生电场的电场线(其中方向未标出)的分布如图所示.图中O点为两点电荷连线的中点,MN为两点电荷连线的中垂线,点P在MN上.电场线的分布关于MN左右对称.下列说法中正确的是( )
如图所示,A、B两个点电荷在真空中所产生电场的电场线(其中方向未标出)的分布如图所示.图中O点为两点电荷连线的中点,MN为两点电荷连线的中垂线,点P在MN上.电场线的分布关于MN左右对称.下列说法中正确的是( )
 如图所示,A、B两个点电荷在真空中所产生电场的电场线(其中方向未标出)的分布如图所示.图中O点为两点电荷连线的中点,MN为两点电荷连线的中垂线,点P在MN上.电场线的分布关于MN左右对称.下列说法中正确的是( )
如图所示,A、B两个点电荷在真空中所产生电场的电场线(其中方向未标出)的分布如图所示.图中O点为两点电荷连线的中点,MN为两点电荷连线的中垂线,点P在MN上.电场线的分布关于MN左右对称.下列说法中正确的是( )| A. | 这两个点在电荷为等量同种电荷 | B. | 这两个点电荷为等量异种电荷 | ||
| C. | O点的电场强度比P点的电场强度大 | D. | O点的电场强度比P点的电场强度小 |
16. 如图为一种服务型机器人,其额定功率为48w,额定工作电压为24V.机器人的锂电池容量为20A•h.则机器人( )
如图为一种服务型机器人,其额定功率为48w,额定工作电压为24V.机器人的锂电池容量为20A•h.则机器人( )
 如图为一种服务型机器人,其额定功率为48w,额定工作电压为24V.机器人的锂电池容量为20A•h.则机器人( )
如图为一种服务型机器人,其额定功率为48w,额定工作电压为24V.机器人的锂电池容量为20A•h.则机器人( )| A. | 额定工作电流为20A | |
| B. | 充满电后最长工作时间为2h | |
| C. | 电池充满电后总电量为7.2×104C | |
| D. | 以额定电流工作时每秒消耗能量为20J |
14.根据给出的物体的速度和加速度的正、负,下列对物体运动的判断正确的是( )
| A. | 若v0>0、a<0,则物体做加速运动 | B. | 若v0<0、a<0,则物体做加速运动 | ||
| C. | 若v0<0、a>0,则物体做减速运动 | D. | 若v0>0、a>0,则物体做加速运动 |
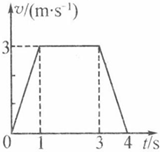 某物体运动的速度图象如图所示,根据图象求:
某物体运动的速度图象如图所示,根据图象求: