题目内容
17.某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,已知电源频率为50Hz,在纸带上确定出A、B、C、D、E、F、G共七个计数点,每两个计数点间有四个点未画出,相邻计数点间的距离如图所示,则打下计数点D时瞬时速度v=0.56m/s,运动过程中的加速度a=0.80m/s2(计算结果均保留两位有效数字)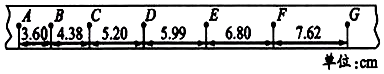
分析 根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小.根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小.
解答 解:根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小.
vD=$\frac{{x}_{CE}}{2T}$=$\frac{5.20+5.99}{2×0.1}$×0.01m/s=0.56m/s
设A到B之间的距离为x1,以后各段分别为x2、x3、x4、x5、x6,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,得:
x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值
得:a=$\frac{1}{3}$(a1+a2+a3)=$\frac{{x}_{DG}+{x}_{AD}}{9{T}^{2}}$=$\frac{(7.62+6.80+5.99)-(3.62+4.38+5.20)}{9×0.{1}^{2}}$×0.01m/s=0.80m/s2
故答案为:0.56,0.80.
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,同时注意有效数字的保留.

练习册系列答案
相关题目
12. 如图所示,板长为L的平行板电容器与一直流电源相连接,其极板与水平面成300角;若粒子甲乙以相同的大小的初速度v0=$\sqrt{2gL}$,由图中的P点射入电容器,分别沿着虚线1和2运动,然后离开电容器;虚线1为连接上下极板边缘的水平线,虚线2为平行且靠近上极板的直线,则下列关于两粒子的说法正确的是( )
如图所示,板长为L的平行板电容器与一直流电源相连接,其极板与水平面成300角;若粒子甲乙以相同的大小的初速度v0=$\sqrt{2gL}$,由图中的P点射入电容器,分别沿着虚线1和2运动,然后离开电容器;虚线1为连接上下极板边缘的水平线,虚线2为平行且靠近上极板的直线,则下列关于两粒子的说法正确的是( )
 如图所示,板长为L的平行板电容器与一直流电源相连接,其极板与水平面成300角;若粒子甲乙以相同的大小的初速度v0=$\sqrt{2gL}$,由图中的P点射入电容器,分别沿着虚线1和2运动,然后离开电容器;虚线1为连接上下极板边缘的水平线,虚线2为平行且靠近上极板的直线,则下列关于两粒子的说法正确的是( )
如图所示,板长为L的平行板电容器与一直流电源相连接,其极板与水平面成300角;若粒子甲乙以相同的大小的初速度v0=$\sqrt{2gL}$,由图中的P点射入电容器,分别沿着虚线1和2运动,然后离开电容器;虚线1为连接上下极板边缘的水平线,虚线2为平行且靠近上极板的直线,则下列关于两粒子的说法正确的是( )| A. | 两者均做匀减速直线运动 | |
| B. | 两者电势能均逐渐增加 | |
| C. | 两者的比荷之比为3:4 | |
| D. | 两者离开电容器时的速率之比为v甲:v乙=$\sqrt{2}:\sqrt{3}$ |
6.在狭义相对论中,下列说法中正确的是( )
| A. | 经典物理学可视为相对论在低速运动时的特例 | |
| B. | 真空中的光速在不同的惯性参考系中是不相同的 | |
| C. | 一条沿自身长度方向运动的杆,其长度总比杆静止时的长度大 | |
| D. | 狭义相对论全面否定了经典物理学 |
7.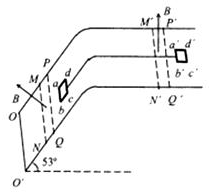 如图所示,倾角53°的绝缘斜面与绝缘水平面平滑对接,斜面及水平面上的矩形区域MNPQ、M′N′P′Q′内有磁感应强度大小均为B,方向垂直于各自表面向上的匀强磁场,磁场宽度$\overline{NQ}$=$\overline{N′Q′}$=L.abcd、a′b′c′d′是两个完全相间的正方形导线框,其质量均为m、边长均为L,两框通过不可伸长的绝缘轻线相连后,分别置子于斜面和水平面上,ab∥a′b′∥MN∥M′N′∥OO′.开始时 锁定a′b′c′d′框,此时ab与PQ、a′b′与P′Q′的距离也为L.解除锁定,两框一起运动,恰好能匀速通过磁场.己知两框与表面的动摩檫因数均为0.25.不计轻线与表面的摩擦,重力加速度为g.sin53°=0.8,cos53°=0.6,下列判断正确的是( )
如图所示,倾角53°的绝缘斜面与绝缘水平面平滑对接,斜面及水平面上的矩形区域MNPQ、M′N′P′Q′内有磁感应强度大小均为B,方向垂直于各自表面向上的匀强磁场,磁场宽度$\overline{NQ}$=$\overline{N′Q′}$=L.abcd、a′b′c′d′是两个完全相间的正方形导线框,其质量均为m、边长均为L,两框通过不可伸长的绝缘轻线相连后,分别置子于斜面和水平面上,ab∥a′b′∥MN∥M′N′∥OO′.开始时 锁定a′b′c′d′框,此时ab与PQ、a′b′与P′Q′的距离也为L.解除锁定,两框一起运动,恰好能匀速通过磁场.己知两框与表面的动摩檫因数均为0.25.不计轻线与表面的摩擦,重力加速度为g.sin53°=0.8,cos53°=0.6,下列判断正确的是( )
 如图所示,倾角53°的绝缘斜面与绝缘水平面平滑对接,斜面及水平面上的矩形区域MNPQ、M′N′P′Q′内有磁感应强度大小均为B,方向垂直于各自表面向上的匀强磁场,磁场宽度$\overline{NQ}$=$\overline{N′Q′}$=L.abcd、a′b′c′d′是两个完全相间的正方形导线框,其质量均为m、边长均为L,两框通过不可伸长的绝缘轻线相连后,分别置子于斜面和水平面上,ab∥a′b′∥MN∥M′N′∥OO′.开始时 锁定a′b′c′d′框,此时ab与PQ、a′b′与P′Q′的距离也为L.解除锁定,两框一起运动,恰好能匀速通过磁场.己知两框与表面的动摩檫因数均为0.25.不计轻线与表面的摩擦,重力加速度为g.sin53°=0.8,cos53°=0.6,下列判断正确的是( )
如图所示,倾角53°的绝缘斜面与绝缘水平面平滑对接,斜面及水平面上的矩形区域MNPQ、M′N′P′Q′内有磁感应强度大小均为B,方向垂直于各自表面向上的匀强磁场,磁场宽度$\overline{NQ}$=$\overline{N′Q′}$=L.abcd、a′b′c′d′是两个完全相间的正方形导线框,其质量均为m、边长均为L,两框通过不可伸长的绝缘轻线相连后,分别置子于斜面和水平面上,ab∥a′b′∥MN∥M′N′∥OO′.开始时 锁定a′b′c′d′框,此时ab与PQ、a′b′与P′Q′的距离也为L.解除锁定,两框一起运动,恰好能匀速通过磁场.己知两框与表面的动摩檫因数均为0.25.不计轻线与表面的摩擦,重力加速度为g.sin53°=0.8,cos53°=0.6,下列判断正确的是( )| A. | 刚进入磁场时,ab边感应电流的方向由a至b | |
| B. | 刚进入磁场时,abcd框克服安培力做功的功率为$\frac{13mg\sqrt{10gL}}{100}$ | |
| C. | 两导线框的电阻均为$\frac{{B}^{2}{L}^{2}}{mg}$$\sqrt{10gl}$ | |
| D. | 从开始运动到cd边刚好离开磁场,经历的时间为2$\sqrt{\frac{10L}{g}}$ |
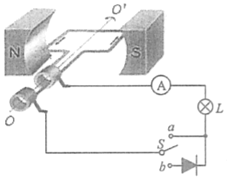 如图所示,一匝数为N=100匝的矩形线圈,面积S=0.0lm2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=$\frac{\sqrt{2}}{10}$T,线圈通过滑环接一标有“6V 3W”
如图所示,一匝数为N=100匝的矩形线圈,面积S=0.0lm2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=$\frac{\sqrt{2}}{10}$T,线圈通过滑环接一标有“6V 3W”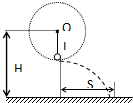 如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求:
如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求: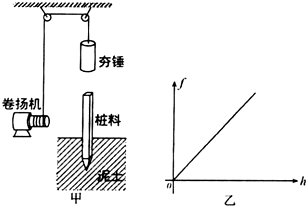 如图甲所示,是建筑工地将桩料打入泥土中以加固地基的打夯机示意图,打夯前先将桩料扶正立于地基上.已知夯锤的质量为M=450kg,桩料的质量为m=50kg.每次打夯都通过卷扬机牵引将夯锤提升到距离桩顶h0=5m处再释放,让夯锤自由下落,夯锤砸在桩料上并不弹起,而是随桩料一起向下运动.桩料进入泥土后所受阻力随打入深度h的变化关系如图乙所示,直线斜率k=5.05×104N/m.g=10m/s2,求
如图甲所示,是建筑工地将桩料打入泥土中以加固地基的打夯机示意图,打夯前先将桩料扶正立于地基上.已知夯锤的质量为M=450kg,桩料的质量为m=50kg.每次打夯都通过卷扬机牵引将夯锤提升到距离桩顶h0=5m处再释放,让夯锤自由下落,夯锤砸在桩料上并不弹起,而是随桩料一起向下运动.桩料进入泥土后所受阻力随打入深度h的变化关系如图乙所示,直线斜率k=5.05×104N/m.g=10m/s2,求