题目内容
一个摆长为l1的单摆，在地面上做简谐运动，周期为T1，已知地球质量为M1，半径为R1，另一摆长为l2的单摆，在质量为M2，半径为R2的星球表面做简谐运动，周期为T2，若T1＝2T2，l1＝4l2，M1＝4M2，则地球半径与星球半径之比R1∶R2为（ ）
| A．2∶1 | B．2∶3 | C．1∶2 | D．3∶2 |
A
解析试题分析：由单摆的周期公式
有：
，代入已知条件可得
，由万有引力定律和牛顿第二定律有
，即：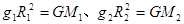
，代入数据解得
，故只有选项A正确；
考点：万有引力定律及其应用、单摆周期公式
，
，
科学家在地球轨道外侧发现了一颗绕太阳运行的小行星，经过观测该小行星每隔t时间与地球相距最近，已知地球绕太阳公转的半径为R、公转周期为T，设地球和小行星运行轨道都是圆轨道，万有引力常量为G，由以上信息不能求出的物理量是
| A．小行星的质量 | B．太阳的质量 |
| C．小行星的公转周期 | D．小行星的公转轨道半径 |
我国未来将在月球地面上建立月球基地，并在绕月轨道上建造空间站．如图所示，关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近，并将在椭圆轨道的近月点B处与空间站C对接．已知空间站绕月圆轨道的半径为r，周期为T，万有引力常量为G，月球的半径为R．下列说法错误的是（ ）
| A．要使对接成功，飞机在接近B点时必须减速 |
| B．航天飞机在图示位置正在加速向B运动 |
C．月球的质量为 |
D．月球的第一宇宙速度为 |
2013年12月2日1时30分，西昌卫星发射中心用“长征三号乙”运载火箭成功将“嫦娥三号”探测器发射升空。卫星由地面发射后，进入地月转移轨道，经过P点时变轨进入距离月球表面100公里圆形轨道I，在轨道I上经过Q点时变轨进入椭圆轨道II，轨道II与月球相切于M点， “玉兔号”月球车将在M点着陆月球表面。
| A．“嫦娥三号”在轨道I上的运动速度比月球的第一宇宙速度小 |
| B．“嫦娥三号”在地月转移轨道上经过P点的速度比在轨道Ⅰ上经过P点时大 |
| C．“嫦娥三号”在轨道II上运动周期比在轨道I上短 |
| D．“嫦娥三号”在轨道Ⅰ上经过Q点时的加速度小于在轨道Ⅱ上经过Q点时的加速度 |
假设月球半径为R，月球表面的重力加速度为g0。如图所示，飞船首先沿距月球表面高度为3R的圆轨道I运动，到达轨道的A点时点火变轨进入椭圆轨道II，到达轨道II的近月点B再次点火进入近月轨道III(轨道半径可近似当做R)绕月球做圆周运动。下列判断正确的是（ ）
A．飞船在轨道I上的运行速率为 |
B．飞船在轨道III绕月球运动一周所需的时间为 |
| C．飞船在A点点火变轨的瞬间，速度减小 |
| D．飞船在A点的线速度大于在B点的线速度 |
某同学在物理学习中记录了一些与地球、月球有关的数据资料如下：地球半径R＝6400km，月球半径r＝1740km，地球表面重力加速度g0＝9.80m／s2，月球表面重力加速度g′＝1.56m／s2，月球绕地球中心转动的线速度v＝l km／s，月球绕地球转动一周时间为T＝27.3天，光速c＝2.998×105km／s.1969年8月1日第一次用激光器向位于头顶的月球表面发射出激光光束，经过约t=2.565s接收到从月球表面反射回来的激光信号，利用上述数据可估算出地球表面与月球表面之间的距离s，则下列方法正确的是（ ）
A．利用激光束的反射s＝c· 来算 |
B．利用v＝ 来算 |
C．利用 g0＝ 来算 |
D．利用 ＝ (s＋R＋r)来算 |
“嫦娥三号”任务是我国探月工程“绕、落、回”三步走中的第二步，“嫦娥三号”分三步实现了在月球表面平稳着陆。一、从100公里×100公里的绕月圆轨道上，通过变轨进入100公里×15公里的绕月椭圆轨道；二、着陆器在15公里高度开启发动机反推减速，进入缓慢的下降状态，到100米左右着陆器悬停，着陆器自动判断合适的着陆点；三、缓慢下降到距离月面4米高度时无初速自由下落着陆。下图是“嫦娥三号”飞行轨道示意图（悬停阶段示意图未画出）。下列说法错误的是（ ）
| A．“嫦娥三号”在椭圆轨道上的周期小于圆轨道上的周期 |
| B．“嫦娥三号”在圆轨道和椭圆轨道经过相切点时的加速度相等 |
| C．着陆器在100米左右悬停时处于失重状态 |
| D．着陆瞬间的速度一定小于9m/s |
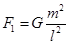