题目内容
“嫦娥三号”任务是我国探月工程“绕、落、回”三步走中的第二步，“嫦娥三号”分三步实现了在月球表面平稳着陆。一、从100公里×100公里的绕月圆轨道上，通过变轨进入100公里×15公里的绕月椭圆轨道；二、着陆器在15公里高度开启发动机反推减速，进入缓慢的下降状态，到100米左右着陆器悬停，着陆器自动判断合适的着陆点；三、缓慢下降到距离月面4米高度时无初速自由下落着陆。下图是“嫦娥三号”飞行轨道示意图（悬停阶段示意图未画出）。下列说法错误的是（ ）
| A．“嫦娥三号”在椭圆轨道上的周期小于圆轨道上的周期 |
| B．“嫦娥三号”在圆轨道和椭圆轨道经过相切点时的加速度相等 |
| C．着陆器在100米左右悬停时处于失重状态 |
| D．着陆瞬间的速度一定小于9m/s |
C
解析试题分析：据题意，“嫦娥三号”在椭圆轨道上的周期和在圆轨道上的周期可以通过开普勒第三定律分析，即
，由于
，则
，故选项A正确；据向心加速度
可知，切点加速度相等，故选项B正确；当着陆器处于悬停状态时受力平衡，故选项C错误；由于着陆瞬间做自由落体运动，则着陆瞬间速度为：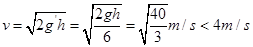
，故选项D正确。
考点：本题考查万有引力定律。
2013年6月20日，我国首次实现太空授课，航天员王亚平在飞船舱内与地面学生实时交流了51分钟。设飞船舱内王亚平的质量为m，用R表示地球的半径，用r表示飞船的轨道半径，g表示地球表面处的重力加速度，g′ 表示飞船所在处的重力加速度，用F表示飞船舱内王亚平受到地球的引力，则下列关系式中正确的是：（ ）
| A．g′=0 | B． | C．F=mg | D． |
一个摆长为l1的单摆，在地面上做简谐运动，周期为T1，已知地球质量为M1，半径为R1，另一摆长为l2的单摆，在质量为M2，半径为R2的星球表面做简谐运动，周期为T2，若T1＝2T2，l1＝4l2，M1＝4M2，则地球半径与星球半径之比R1∶R2为（ ）
| A．2∶1 | B．2∶3 | C．1∶2 | D．3∶2 |
已知引力常数为G，月球中心到地球中心的距离为R和月球绕地球运行的周期为T。仅利用这三个数据，可以估算出的物理量有（ ）
| A．月球的质量 | B．地球的质量 |
| C．月球绕地球运行速度的大小 | D．地球的半径 |
2013年12月6日17时47分，在北京飞控中心工作人员的精密控制下，嫦娥三号开始实施近月制动，进入100公里环月轨道Ⅰ，2013年12月10日晚21:20分左右，嫦娥三号探测器将再次变轨，从100公里的环月圆轨道Ⅰ，降低到近月点（B点）15公里、远月点（A点）100公里的椭圆轨道Ⅱ，为下一步月面软着陆做准备．关于嫦娥三号卫星下列说法不正确的是 （ ）
| A．卫星在轨道Ⅱ上A点的加速度小于在B点的加速度 |
| B．卫星A点到B点处于失重状态，从B点到A点处于超重状态 |
| C．卫星从轨道Ⅰ变轨到轨道Ⅱ火箭对它做了负功 |
| D．卫星在轨道Ⅱ经过A点时的机械能等于在轨道Ⅱ经过B点时机械能 |
已知引力常量G和下列各组数据，能计算出地球质量的是
| A．地球绕太阳运行的周期T及地球离太阳的距离r |
| B．月球绕地球运行的周期T及月球离地球的距离r |
| C．人造地球卫星在地面附近绕行的速度v及运行周期T |
| D．已知地球表面重力加速度g(不考虑地球自转) |
在牛顿发现万有引力定律一百多年之后，卡文迪许首先精确测量了引力常量。在国际单位制中引力常量的单位是
| A．N·kg2 | B．N·m2 |
| C．N·kg2/m2 | D．N·m2/kg2 |
若已知行星绕太阳公转的半径为r，公转的周期为T，万有引力恒量为G，则由此可求出（ ）
| A．某行星的质量 | B．太阳的质量 |
| C．某行星的密度 | D．太阳的密度 |
在“嫦娥一号”奔月飞行过程中，在月球上空有一次变轨是由椭圆轨道a变为近月圆形轨道b，如图所示.在a、b切点处,下列说法正确的是 
| A．卫星运行的速度va > vb | B．卫星受月球的引力Fa = Fb |
| C．卫星的加速度 aa > ab | D．卫星的动能Eka< Ekb |